
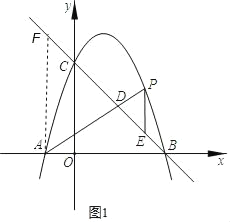
����Ŀ����ͼ����ƽ��ֱ�������У�������y��ax2+bx+c����A����1��0����B��3��0����C��0��3������P��ֱ��BC�Ϸ��������ϵ�һ���㣬PE��y�ᣬ��ֱ��BC�ڵ�E����AP����ֱ��BC�ڵ� D��
��1���������ߵĺ�������ʽ��
��2����AD��2PDʱ�����P�����ꣻ
��3�����߶�PE�����ֵ��
��4�����߶�PE���ʱ������F��ֱ��BC���ҡ�EFP��2��ACO��ֱ��д����F�����꣮

���𰸡���1��y����x2+2x+3����2��P��1��4����P��2��3������3������![]() ����
����![]() ��
��
��������
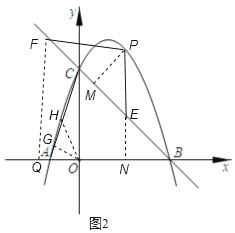
��1��������������x�����������������֪���ɰ������ߵĽ���ʽ��ɽ���ʽ���ٴ�����һ��֪���������������ʽ��
��2����A��EF��x�ᣬ��BC�ཻ�ڵ�F���ô���ϵ�������BC�Ľ���ʽ����P��ĺ�����Ϊt���������AF��PE�������������εı����߶����t��ɣ�
��3������PE����t�ĺ�������ʽ���ɺ�����������������ֵ��ɣ�
��4��������������ٵ�F����PE�����ʱ������P��PM��BC�ڵ�M����E��EN��x���ڵ�N������F��FQ��x���ڵ�Q������O��OG��AC�ڵ�G��ȡAC���е�H������OH��ͨ���������������MF��ֵ��ɣ��ڽ���õ�F�����꣬����PM�ԳƵ������һF�㣮
��1���������ߵĽ���ʽΪ��y��a��x+1����x��3����a��0����
��3��a��1������3����
��a����1��
�������ߵĽ���ʽΪ��y������x+1����x��3����
��y����x2+2x+3��
��2����A��EF��x�ᣬ��BC�ཻ�ڵ�F����ͼ1����P��t����t2+2t+3����
��AF��PE��
��BC�Ľ���ʽΪy��kx+b��k��0����
��![]() ��
��
���![]() ��
��
��ֱ��BC�Ľ���ʽΪ��y����x+3��
��E��t����t+3����F����1��4����
��AF��4��PE����t2+3t��
��AF��PE��
���AFD�ס�PED��
��![]() ��
��
��AD��2PD��
��![]() ��
��
��ã�t��1��2��
��P��1��4����P��2��3����
��3����PE�Ľ���ʽΪ��PE����t2+3t������t��![]() ��2+
��2+![]() ��0��t��3����
��0��t��3����
�൱t��![]() ʱ��PE��ֵ���Ϊ
ʱ��PE��ֵ���Ϊ![]() ��
��
��4���ٵ�F����PE�����ʱ��
����P��PM��BC�ڵ�M����E��EN��x���ڵ�N������F��FQ��x���ڵ�Q������O��OG��AC�ڵ�G��ȡAC���е�H������OH��
�ɣ�3��֪����PEȡ���ֵʱ��P��![]() ��
��![]() ����PE��
����PE��![]() ��E��
��E��![]() ��
��![]() ����
����
��OB��OC��3��
���OBC����OCB��45����
��BE��![]() EM��
EM��![]() ����PEM��45����
����PEM��45����
��PM��EM��![]() ��
��
��AC��![]() ��
��
��OH��CH��![]() ��
��
OG��![]() ��
��
��HG��![]() ����OHG��2��ACO��
����OHG��2��ACO��
�ߡ�EFP��2��ACO��
���EFP����OHG��
�ߡ�OGH����PMF��
���OGH�ס�PMF��
��![]() ����
����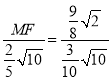 ��
��
��MF��![]() ��
��
��BF��BE+EM+MF��![]() ��
��
��FQ��BQ��![]() BF��
BF��![]() ��
��
��OQ��![]() ��
��
��F����![]() ��
��![]() ����
����
�ڵ�F����PE���ұ�ʱ����ʱ��F��ǡ���루��![]() ��
��![]() ������PM�Գƣ������ʱF��
������PM�Գƣ������ʱF��![]() ��
��![]() ����
����
��F����������![]() ��
��![]() ����
����![]() ��
��![]() ����
����


 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��ס��ҡ�������ҵ��Ա2018��ǰ5���µ����۶��λ����Ԫ�����±���
�·� ���۶� ��Ա | ��1�� | ��2�� | ��3�� | ��4�� | ��5�� |
�� | 6 | 9 | 10 | 8 | 8 |
�� | 5 | 7 | 8 | 9 | 9 |
�� | 5 | 9 | 10 | 5 | 11 |
��1�������ϱ��е����ݣ����±�����������
ͳ��ֵ ��ֵ ��Ա | ƽ��������Ԫ�� | ��������Ԫ�� | ��λ������Ԫ�� | ���� |
�� | 8 | 8 | 1.76 | |
�� | 7.6 | 8 | 2.24 | |
�� | 8 | 5 |
��2���ס��ҡ�������ҵ��Ա��˵�Լ�������ҵ���ã�����ͬ˭��˵������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
�У�![]() Ϊֱ����
Ϊֱ����![]() �ң�
�ң�![]() ����Ϊ
����Ϊ![]() ����
����![]() Ϊ
Ϊ![]() ���е㣬����
���е㣬����![]() ��
��
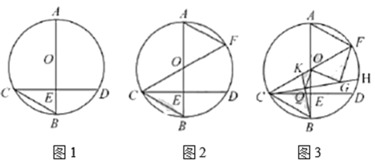
��1����ͼ1����![]() �Ķ�����
�Ķ�����
��2����ͼ2������![]() ���ӳ�����Բ
���ӳ�����Բ![]() �ڵ�
�ڵ�![]() ������
������![]() ����֤��
����֤��![]()
��3���ڣ�2���ʵ������£�![]() Ϊ��
Ϊ��![]() �ϵ�һ�㣬����
�ϵ�һ�㣬����![]() ��
��![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() �ϵ�һ�㣬����
�ϵ�һ�㣬����![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ�����ɼ��㡢����ͼ�����ɵ�����ϵ����������ϵ����ͼ����ƽ����ȡ��һ��O��Ϊ���㣻�ӵ�O������һ������Ox��Ϊ����߶�OM�ij��ȳ�Ϊ��������M�ļ�����Ϳ������߶�OM�ij����Լ���Oxת����OM�ĽǶȣ��涨��ʱ�뷽��ת���Ƕ�Ϊ������ȷ������M��4��30������M��4��-330������M��4��390�����ȣ�������˵���������ǣ� ����
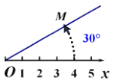
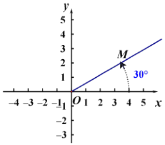
A.��M����x��ԳƵ�M1�ļ�������Ա�ʾΪM1��4��-30����
B.��M����ԭ��O���ĶԳƵ�M2�ļ�������Ա�ʾΪM2��4��570����
C.�Լ���Ox����ֱ��Ϊx�Ὠ����ͼ��ʾ��ƽ��ֱ������ϵ��������M��4��30����ת��Ϊƽ��ֱ�����������ΪM��2��2![]() ��
��
D.��ƽ��ֱ������ϵ�еĵ�N��-4��4��ת��Ϊ�����꣬�ɱ�ʾΪN��![]() ��135����
��135����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����¥AD����CB֮��ľ���AC��Ϊ27m��ij����¥��A���������������Ϊ60��������¥��D���������B������Ϊ30�����ֱ����¥AD�ĸ�����BC�ĸ��������ȷ��0.1m���ο����ݣ�![]() ��2.24��
��2.24��![]() ��1.732��
��1.732��![]() ��1.414��
��1.414��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=3��BC=4������P��A���������A��B��C�ķ�����AB��BC���ƶ�����PA=x����D��ֱ��PA�ľ���Ϊy����y����x�ĺ���ͼ������ǣ� ��

A. B.
B.
C. D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��Rt��ABC�����Բ����ACB=90������D��![]() �ϵ�һ�㣬��
�ϵ�һ�㣬��![]() ������AD��BC�ڵ�F������A����O������AE��BC���ӳ����ڵ�E��
������AD��BC�ڵ�F������A����O������AE��BC���ӳ����ڵ�E��
��1����֤��CF=CE��
��2����AD=8��AC=5�����O�İ뾶��
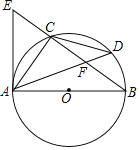
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O����O��AB�ϣ�BC=CD������C����O�����ߣ��ֱ�AB��AD���ӳ����ڵ�E��F��
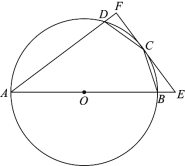
��1����֤��AF��EF����2����cosA=![]() ��BE=1����AD�ij���
��BE=1����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������ABC�У�AB=AC,AE�ǽ�ƽ���ߣ�BMƽ����ABC��AE�ڵ�M,����B,M�������O��BC�ڵ�G,��AB�ڵ�F,FBǡΪ��O��ֱ��.

��1����֤��AE����O���У�
��2����BC=4,cosC=![]() ʱ������O�İ뾶.
ʱ������O�İ뾶.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com