
【题目】在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OM的长度称为极径.点M的极坐标就可以用线段OM的长度以及从Ox转动到OM的角度(规定逆时针方向转动角度为正)来确定,即M(4,30°)或M(4,-330°)或M(4,390°)等,则下列说法错误的是( ).
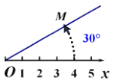
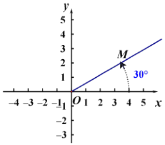
A.点M关于x轴对称点M1的极坐标可以表示为M1(4,-30°)
B.点M关于原点O中心对称点M2的极坐标可以表示为M2(4,570°)
C.以极轴Ox所在直线为x轴建立如图所示的平面直角坐标系,则极坐标M(4,30°)转化为平面直角坐标的坐标为M(2,2![]() )
)
D.把平面直角坐标系中的点N(-4,4)转化为极坐标,可表示为N(![]() ,135°)
,135°)
【答案】C
【解析】
A、B选项,先根据对称的性质确定对称点位置,再得出极坐标;C、D选项,过点M作x轴的垂线,根据勾股定理得出平面直角坐标与极坐标的关系.
A中,点![]() 与点M关于x轴对称,则点
与点M关于x轴对称,则点![]() 在第四象限,极坐标为(4,-30°)
在第四象限,极坐标为(4,-30°)
B中,点![]() 与点M关于原点对称,则点
与点M关于原点对称,则点![]() 在第三象限,极坐标为(4,(30+180)°),根据极坐标的特点,将角度加360°,结果不变,则
在第三象限,极坐标为(4,(30+180)°),根据极坐标的特点,将角度加360°,结果不变,则![]() 可表示为(4,(30+180+360)°),即(4,570°);
可表示为(4,(30+180+360)°),即(4,570°);
C中,如下图,过点M作x轴的垂线

∵OM=4,∠MON=30°,∴在Rt△MON中,ON=2![]() ,MN=2,∴M(2
,MN=2,∴M(2![]() ,2);
,2);
D中,如下图,过点N作x轴的垂线
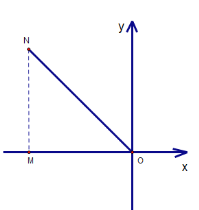
∵N(-4,4),∴NM=4,MO=4
∴∠NOM=45°,ON=4![]() ,∴∠NOX=135°
,∴∠NOX=135°
∴N(4![]() ,135°)
,135°)
故选:C


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小夏同学从家到学校有![]() ,
,![]() 两条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
两条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时 频数 公交车路线 |
|
|
|
| 总计 |
| 59 | 151 | 166 | 124 | 500 |
| 43 | 57 | 149 | 251 | 500 |
据此估计,早高峰期间,乘坐![]() 线路“用时不超过35分钟”的概率为__________,若要在40分钟之内到达学校,应尽量选择乘坐__________(填
线路“用时不超过35分钟”的概率为__________,若要在40分钟之内到达学校,应尽量选择乘坐__________(填![]() 或
或![]() )线路.
)线路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数![]() ,一次函数
,一次函数![]() ,若方程
,若方程![]() 的两根是
的两根是![]() ,
,![]() .
.
(1)求b、c的值;
(2)当x满足![]() 时,比较
时,比较![]() 与x的大小并说明理由;
与x的大小并说明理由;
(3)设点M的坐标是![]() ,点P是抛物线
,点P是抛物线![]() 上的一个动点,当点P到点M的距离与到直线
上的一个动点,当点P到点M的距离与到直线![]() 的距离之和最小时,请直接写出点P坐标.
的距离之和最小时,请直接写出点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更好开展“课后延时”服务,某校抽取了部分七年级学生,就课后活动项目进行调查.学校根据学生前期统计给出了如下四个选项:![]() “球类”、
“球类”、![]() “棋类”、
“棋类”、![]() “计算机信息类”、
“计算机信息类”、![]() “其他”,并将最终调查结果绘制成如下两幅不完整的统计图.
“其他”,并将最终调查结果绘制成如下两幅不完整的统计图.

根据图中提供的信息,解决下列问题:
(1)本次调查共抽取了____名学生,扇形统计图中,![]() 类所对应的扇形圆心角大小为
类所对应的扇形圆心角大小为
(2)将条形统计图补充完整;
(3)已知选择![]() 类的同学有两位来自七(1)班,其余来自七(2)班,调查组准备从选
类的同学有两位来自七(1)班,其余来自七(2)班,调查组准备从选![]() 类同学中任选两位做细致分析求两位同学来自同一个班级的概率.
类同学中任选两位做细致分析求两位同学来自同一个班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
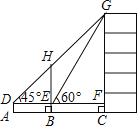
【题目】如图,某数学兴趣小组利用一棵古树BH测量教学楼CG的高,先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为45°,此时教学楼顶端G恰好在视线DH上,再向前走7米到达B处,又测得教学楼顶端G的仰角∠GEF为60°,点A、B、C三点在同一水平线上.计算教学楼CG的高.(结果精确到0.1,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
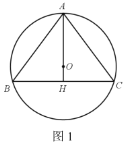
【题目】如图1,已知,⊙O是△ABC的外接圆,AB=AC=10,BC=12,连接AO并延长交BC于点H.
(1)求外接圆⊙O的半径;
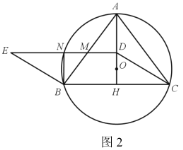
(2)如图2,点D是AH上(不与点A,H重合)的动点,以CD,CB为边,作平行四边形CDEB,DE分别交⊙O于点N,交AB边于点M.
①连接BN,当BN⊥DE时,求AM的值;
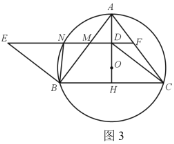
②如图3,延长ED交AC于点F,求证:NM·NF=AM·MB;
③设AM=x,要使![]() -2
-2![]() <0成立,求x的取值范围.
<0成立,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),C(0,3),点P是直线BC上方抛物线上的一动点,PE∥y轴,交直线BC于点E连接AP,交直线BC于点 D.
(1)求抛物线的函数表达式;
(2)当AD=2PD时,求点P的坐标;
(3)求线段PE的最大值;
(4)当线段PE最大时,若点F在直线BC上且∠EFP=2∠ACO,直接写出点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=-x2+(m-1) x+m (m为常数),其顶点为M.
(1)请判断该函数的图像与x轴公共点的个数,并说明理由;
(2)当-2≤m≤3时,求该函数的图像的顶点M纵坐标的取值范围;
(3)在同一坐标系内两点A(-1,-1)、B(1,0),△ABM的面积为S,当m为何值时,S的面积最小?并求出这个最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com