
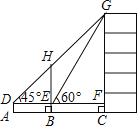
【题目】如图,某数学兴趣小组利用一棵古树BH测量教学楼CG的高,先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为45°,此时教学楼顶端G恰好在视线DH上,再向前走7米到达B处,又测得教学楼顶端G的仰角∠GEF为60°,点A、B、C三点在同一水平线上.计算教学楼CG的高.(结果精确到0.1,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
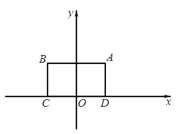
【题目】对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为(![]() ,
,![]() ),顶点C、D在x轴上,且OC=OD.
),顶点C、D在x轴上,且OC=OD.
(1)当⊙P的半径为4时,
①在P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() )中可以成为矩形ABCD的“等距圆”的圆心的是 ;
)中可以成为矩形ABCD的“等距圆”的圆心的是 ;
②如果点P在直线![]() 上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;
上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;
(2)已知点P在![]() 轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.
轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年中考理化实验操作考试,采用学生抽签方式决定自己的考试内容.规定:每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学实验(用纸签D、E、F表示)中各抽取一个进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.
(1) 用“列表法”或“树状图法”表示所有可能出现的结果;
(2) 小刚抽到物理实验B和化学实验F(记作事件P)的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 为直径,
为直径,![]() 弦,
弦,![]() 垂足为
垂足为![]() ,且
,且![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
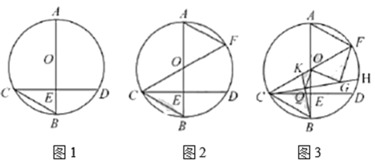
(1)如图1,求![]() 的度数.
的度数.
(2)如图2,连接![]() 并延长,交圆
并延长,交圆![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]()
(3)在(2)问的条件下,![]() 为弧
为弧![]() 上的一点,连接
上的一点,连接![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的一点,连接
上的一点,连接![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们参加综合实践活动时,看到木工师傅用“三弧法”在板材边角处作直角,其作法是:如图:
(1)作线段AB,分别以点A,B为圆心,AB长为半径作弧,两弧交于点C;
(2)以点C为圆心,仍以AB长为半径作弧交AC的延长线于点D;
(3)连接BD,BC.
根据以上作图过程及所作图形,下列结论中错误的是( )

A.∠ABD=90°B.CA=CB=CDC.sinA=![]() D.cosD=
D.cosD=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OM的长度称为极径.点M的极坐标就可以用线段OM的长度以及从Ox转动到OM的角度(规定逆时针方向转动角度为正)来确定,即M(4,30°)或M(4,-330°)或M(4,390°)等,则下列说法错误的是( ).
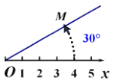
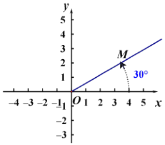
A.点M关于x轴对称点M1的极坐标可以表示为M1(4,-30°)
B.点M关于原点O中心对称点M2的极坐标可以表示为M2(4,570°)
C.以极轴Ox所在直线为x轴建立如图所示的平面直角坐标系,则极坐标M(4,30°)转化为平面直角坐标的坐标为M(2,2![]() )
)
D.把平面直角坐标系中的点N(-4,4)转化为极坐标,可表示为N(![]() ,135°)
,135°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AD与塔CB之间的距离AC长为27m,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶B的仰角为30°,分别求大楼AD的高与塔BC的高(结果精确到0.1m,参考数据:![]() ≈2.24,
≈2.24,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
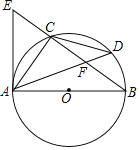
【题目】如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,点D是![]() 上的一点,且
上的一点,且![]() ,连接AD交BC于点F,过点A作⊙O的切线AE交BC的延长线于点E.
,连接AD交BC于点F,过点A作⊙O的切线AE交BC的延长线于点E.
(1)求证:CF=CE;
(2)若AD=8,AC=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象交
的图象交![]() 轴于点
轴于点![]() ,点
,点![]() ,交
,交![]() 轴于点
轴于点![]()

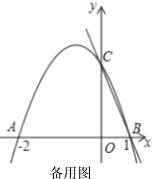
(1)求二次函数的解析式;
(2)连接![]() ,在直线
,在直线![]() 上方的抛物线上有一点
上方的抛物线上有一点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)若点![]() 在
在![]() 轴上,是否存在点
轴上,是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形,若存在,直接写出点
为顶点的三角形是等腰三角形,若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com