
【题目】如图,二次函数![]() 的图象交
的图象交![]() 轴于点
轴于点![]() ,点
,点![]() ,交
,交![]() 轴于点
轴于点![]()

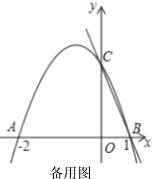
(1)求二次函数的解析式;
(2)连接![]() ,在直线
,在直线![]() 上方的抛物线上有一点
上方的抛物线上有一点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)若点![]() 在
在![]() 轴上,是否存在点
轴上,是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形,若存在,直接写出点
为顶点的三角形是等腰三角形,若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)y=-x2-x+2;(2)l=-n2-2n;(3)存在,(-1,0)或(1+![]() ,0)或(1-
,0)或(1-![]() ,0)或(-
,0)或(-![]() ,0).
,0).
【解析】
(1)利用交点式求二次函数的解析式;
(2)设点N(n,-n2-n+2),则点F(n,n+2),l=-n2-n+2-(n+2)=-n2-2n;
(3)分CB=CM、BC=BM、BM=CM三种情况,分别求解即可.
解:(1)∵二次函数y=ax2+bx+c的图象交x轴于A(-2,0),B(1,0),
设二次函数的解析式为:y=a(x+2)(x-1),
把C(0,2)代入得:2=a(0+2)(0-1),
a=-1,
∴y=-(x+2)(x-1)=-x2-x+2,
故抛物线的表达式为:y=-x2-x+2;
(2)设直线AC的解析式为:y=kx+b,
把A(-2,0)、C(0,2)代入得:![]() ,
,
解得:![]() ,
,
∴直线AC的解析式为:y=x+2,
设点N(n,-n2-n+2),则点F(n,n+2),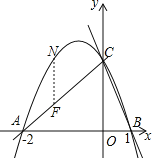
l=-n2-n+2-(n+2)=-n2-2n;
(3)存在,分三种情况:
①如图2,当BC=CM1时,M1(-1,0);

②如图2,由勾股定理得:BC=![]() ,
,
以B为圆心,以BC为半径画圆,交x轴于M2、M3,则BC=BM2=BM3=![]() ,
,
此时,M2(1-![]() ,0),M3(1+
,0),M3(1+![]() ,0);
,0);
③如图3,作BC的中垂线,交x轴于M4,连接CM4,则CM4=BM4,
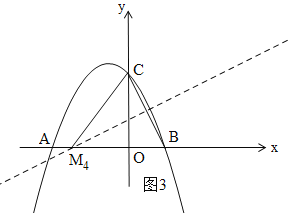
设OM4=x,则CM4=BM4=x+1,
由勾股定理得:22+x2=(1+x)2,
解得:x=![]() ,
,
∵M4在x轴的负半轴上,
∴M4(-![]() ,0),
,0),
综上,点M的坐标为:(-1,0)或(1+![]() ,0)或(1-
,0)或(1-![]() ,0)或(-
,0)或(-![]() ,0).
,0).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
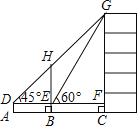
【题目】如图,某数学兴趣小组利用一棵古树BH测量教学楼CG的高,先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为45°,此时教学楼顶端G恰好在视线DH上,再向前走7米到达B处,又测得教学楼顶端G的仰角∠GEF为60°,点A、B、C三点在同一水平线上.计算教学楼CG的高.(结果精确到0.1,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
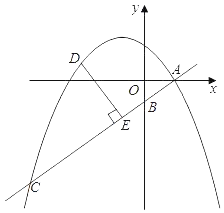
【题目】如图,在平面直角坐标系中,直线y=kx﹣![]() 与抛物线y=ax2+bx+
与抛物线y=ax2+bx+![]() 交于点A、C,与y轴交于点B,点A的坐标为(2,0),点C的横坐标为﹣8.
交于点A、C,与y轴交于点B,点A的坐标为(2,0),点C的横坐标为﹣8.
(1)请直接写出直线和抛物线的解析式;
(2)点D是直线AB上方的抛物线上一动点(不与点A、C重合),作DE⊥AC于点E.设点D的横坐标为m.求DE的长关于m的函数解析式,并写出DE长的最大值;
(3)平移△AOB,使平移后的三角形的三个顶点中有两个在抛物线上,请直接写出平移后的点A对应点A′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
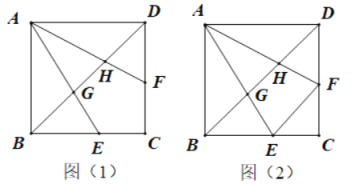
【题目】如图(1),已知正方形ABCD中,点E、F分别在边BC、CD上,BE=DF,AE、AF分别交BD于点G、H.
(1)求证:BG=DH;
(2)连接FE,如图(2),当EF=BG时.
①求证:ADAH=AFDF;
②直接写出![]() 的比值.
的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办学生综合素质大赛,分“单人项目”和“双人项目”两种形式,比赛题目包括下列五类:![]() .人文艺术;
.人文艺术;![]() .历史社会;
.历史社会;![]() .自然科学;
.自然科学;![]() .天文地理;
.天文地理;![]() .体育健康.
.体育健康.
(1)若小明参加“单人项目”,他从中抽取一个题目,那么恰好抽中“自然科学”类题目的概率为_____.
(2)小林和小丽参加“双人项目”,比赛规定:同一小组的两名同学的题目类型不能相同,且每人只能抽取一次,求他们抽到“天文地理”和“体育健康”类题目的概率是多少?(用画树状图或列表的方法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=-x2+(m-1) x+m (m为常数),其顶点为M.
(1)请判断该函数的图像与x轴公共点的个数,并说明理由;
(2)当-2≤m≤3时,求该函数的图像的顶点M纵坐标的取值范围;
(3)在同一坐标系内两点A(-1,-1)、B(1,0),△ABM的面积为S,当m为何值时,S的面积最小?并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
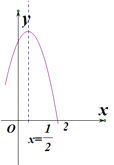
【题目】如图是二次函数![]() 图象的一部分,对称轴为
图象的一部分,对称轴为![]() ,且经过点
,且经过点![]() ,有下列说法:①
,有下列说法:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() 是抛物线上的两点,则
是抛物线上的两点,则![]() ,上述说法正确的是( )
,上述说法正确的是( )
A.①②④B.③④C.①③④D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到.若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=![]() HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.
HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com