
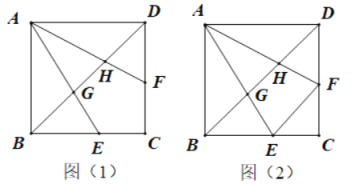
【题目】如图(1),已知正方形ABCD中,点E、F分别在边BC、CD上,BE=DF,AE、AF分别交BD于点G、H.
(1)求证:BG=DH;
(2)连接FE,如图(2),当EF=BG时.
①求证:ADAH=AFDF;
②直接写出![]() 的比值.
的比值.
【答案】(1)见解析; (2) ①见解析; ②![]()
【解析】
(1)根据正方形性质证△ABE≌△ADF(SAS),得∠BAE=∠DAF,再证△ABG≌△ADH(ASA)即可;
(2)①连接GF,证明四边形EBGF是平行四边形,利用BE∥GF∥AD,根据平行线分线段成比例性质可得:![]()
![]() ,
,![]() ,故
,故![]() .
.
②由①可得![]() ,
,![]() ,设CF=k,DF=a,根据勾股定理和 平行线分线段成比例性质得
,设CF=k,DF=a,根据勾股定理和 平行线分线段成比例性质得![]() ,得到
,得到![]() ,再代入化简可得.
,再代入化简可得.
证明:(1)∵四边形 ABCD为正方形
∴AB=AD,∠ABC=∠ADC
∵BE=DF
∴△ABE≌△ADF(SAS)
∴∠BAE=∠DAF
∵AB=AD
∴∠ABD=∠ADB
∴△ABG≌△ADH(ASA)
∴BG=DH
(2)①连接GF.
∵BC=DC,BE=DF,
∴CE=CF
∵∠C=90°
∴∠DBC=∠FEC=45°
∴EF∥BD
∵EF=BG
∴四边形EBGF是平行四边形
∴BE∥GF∥AD
∵AD=CD
∴![]()
![]()
∵EF∥BD
∴![]()
∴![]() ,即
,即![]() .
.
②由(2)可得![]()
∴![]()
∴![]()
设CF=k,DF=a
则EF=![]() ,DG=
,DG=![]() ,
,
∴DH= EF=![]() ,
,
∴GH=![]() -
-![]()
∴由![]() 可得
可得
![]()
整理得
![]()
解得![]()
∴![]()
=
![]()


科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 为直径,
为直径,![]() 弦,
弦,![]() 垂足为
垂足为![]() ,且
,且![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
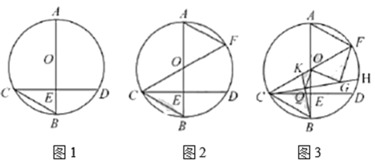
(1)如图1,求![]() 的度数.
的度数.
(2)如图2,连接![]() 并延长,交圆
并延长,交圆![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]()
(3)在(2)问的条件下,![]() 为弧
为弧![]() 上的一点,连接
上的一点,连接![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的一点,连接
上的一点,连接![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,点D是![]() 上的一点,且
上的一点,且![]() ,连接AD交BC于点F,过点A作⊙O的切线AE交BC的延长线于点E.
,连接AD交BC于点F,过点A作⊙O的切线AE交BC的延长线于点E.
(1)求证:CF=CE;
(2)若AD=8,AC=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
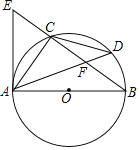
【题目】如图,四边形ABCD内接于⊙O,点O在AB上,BC=CD,过点C作⊙O的切线,分别交AB,AD的延长线于点E,F.
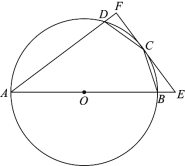
(1)求证:AF⊥EF;(2)若cosA=![]() ,BE=1,求AD的长.
,BE=1,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
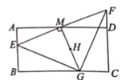
【题目】如图,矩形ABCD中,AB=4,AD=8,点E为AD上一点,将△ABE沿BE折叠得到△FBE,点G为CD上一点,将△DEG沿EG折叠得到△HEG,且E、F、H三点共线,当△CGH为直角三角形时,AE的长为________.
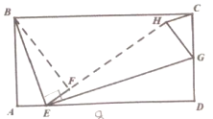
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() ,
,![]() 分别落在点
分别落在点![]() ,
,![]() 处,点
处,点![]() 在
在![]() 轴上,再将
轴上,再将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 轴上,将
轴上,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 轴上,依次进行下去……,若点
轴上,依次进行下去……,若点![]() ,
,![]() ,则点
,则点![]() 的坐标为________.
的坐标为________.
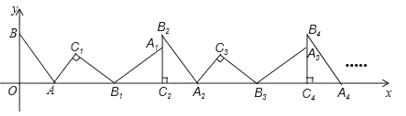
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象交
的图象交![]() 轴于点
轴于点![]() ,点
,点![]() ,交
,交![]() 轴于点
轴于点![]()

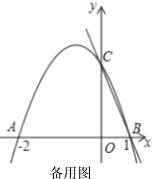
(1)求二次函数的解析式;
(2)连接![]() ,在直线
,在直线![]() 上方的抛物线上有一点
上方的抛物线上有一点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)若点![]() 在
在![]() 轴上,是否存在点
轴上,是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形,若存在,直接写出点
为顶点的三角形是等腰三角形,若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.

(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 是
是![]() 的中点,动点
的中点,动点![]() 在线段
在线段![]() 上,连接
上,连接![]() 并延长交射线
并延长交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,设
,设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() .
.
(1)当点![]() 不与点
不与点![]() 重合时,求证:
重合时,求证:![]() ;
;
(2)①当点![]() 与点
与点![]() 或点
或点![]() 重合时,
重合时,![]() 是等腰直角三角形,当点
是等腰直角三角形,当点![]() 与点
与点![]() 或点
或点![]() 不重合时,请判定
不重合时,请判定![]() 的形状;
的形状;
②求点![]() 移动的最长距离.
移动的最长距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com