
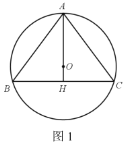
【题目】如图1,已知,⊙O是△ABC的外接圆,AB=AC=10,BC=12,连接AO并延长交BC于点H.
(1)求外接圆⊙O的半径;
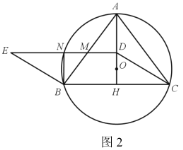
(2)如图2,点D是AH上(不与点A,H重合)的动点,以CD,CB为边,作平行四边形CDEB,DE分别交⊙O于点N,交AB边于点M.
①连接BN,当BN⊥DE时,求AM的值;
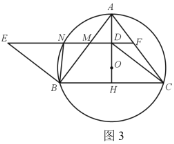
②如图3,延长ED交AC于点F,求证:NM·NF=AM·MB;
③设AM=x,要使![]() -2
-2![]() <0成立,求x的取值范围.
<0成立,求x的取值范围.
【答案】(1)![]() 半径为
半径为![]() ;(2)①
;(2)①![]() ;②详见解析;③当
;②详见解析;③当![]() 时,有
时,有![]() 成立.
成立.
【解析】
(1)如下图,在Rt△ABH中,先求得AH的值,设OA=r,在Rt△OBH中,利用勾股定理可求得r的长;
(2)①如下图,在![]() ,可求得BN的长,然后在矩形NBHD中,求得AD的值,最后利用cos∠MAD求得AM;
,可求得BN的长,然后在矩形NBHD中,求得AD的值,最后利用cos∠MAD求得AM;
②如下图,同过证![]() 可得结论;
可得结论;
③如下图,通过转换,先得出![]()
![]() 这个等式,然后利用
这个等式,然后利用![]() ,设AM=x,可得到关于x的方程,进而求出x的取值范围.
,设AM=x,可得到关于x的方程,进而求出x的取值范围.
解:(1)如图1,连接![]() ,
,
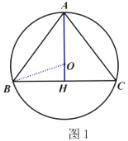
∵![]() 过圆心
过圆心![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
在![]() 中,
中,![]() ,
,
设半径![]() ,则
,则![]() ,在
,在![]() 中,
中,![]() ,
,
解得![]() ,即
,即![]() 半径为
半径为![]() .
.
(2)①如图2,连接![]()
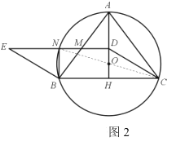
在平行四边形![]() 中,
中,![]() ,∴
,∴![]() .
.
∵![]() ,即
,即![]() ,∴
,∴![]() .
.
∴![]() 是
是![]() 的直径.
的直径.![]() .
.
∴在![]() 中,
中,![]() .
.
∵四边形CDEB是平行四边形,NB⊥BH,DH⊥BH
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,∴
,∴![]() .
.
∴在![]() 中,
中,![]() ,∴
,∴![]() ,
,
②如图3,连接![]() ,
,![]() ,
,

∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
由![]() ,
,![]() 可得
可得![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
∴![]() ,即
,即![]() .
.
③∵![]() ,
,![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]()
![]()
![]()
![]() .
.
∵![]() ,∴
,∴![]() ,
,
由![]() ,得
,得![]() ,
,
∴![]() .
.![]()
该函数图象的示意图如图4
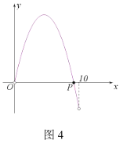
易求得点![]() 坐标为
坐标为![]()
∴当![]() 时,有
时,有![]() 成立.
成立.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]()
![]() 与
与![]() 轴交于点
轴交于点![]() ,其对称轴与
,其对称轴与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() ,
,![]() 的坐标;
的坐标;
(2)设直线![]() 与直线
与直线![]() 关于该抛物线的对称轴对称,
关于该抛物线的对称轴对称,
①求直线![]() 的解析式
的解析式
②若该抛物线在![]() 这一段位于直线
这一段位于直线![]() 的上方,并且在
的上方,并且在![]() 这一段位于直线
这一段位于直线![]() 的下方,求该抛物线的解析式.
的下方,求该抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
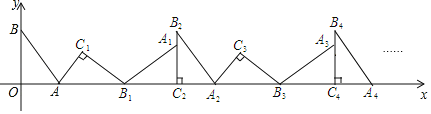
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺指针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…,若点A(![]() ,0)、B(0,4),则点B2020的横坐标为_____.
,0)、B(0,4),则点B2020的横坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
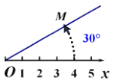
【题目】在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OM的长度称为极径.点M的极坐标就可以用线段OM的长度以及从Ox转动到OM的角度(规定逆时针方向转动角度为正)来确定,即M(4,30°)或M(4,-330°)或M(4,390°)等,则下列说法错误的是( ).
A.点M关于x轴对称点M1的极坐标可以表示为M1(4,-30°)
B.点M关于原点O中心对称点M2的极坐标可以表示为M2(4,570°)
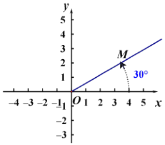
C.以极轴Ox所在直线为x轴建立如图所示的平面直角坐标系,则极坐标M(4,30°)转化为平面直角坐标的坐标为M(2,2![]() )
)
D.把平面直角坐标系中的点N(-4,4)转化为极坐标,可表示为N(![]() ,135°)
,135°)
查看答案和解析>>
科目:初中数学 来源: 题型:
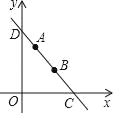
【题目】如图,在平面直角坐标系中,过点A![]() 的直线l分别与x轴、y轴交于点C,D.
的直线l分别与x轴、y轴交于点C,D.
(1)求直线l的函数表达式.
(2)P为x轴上一点,若△PCD为等腰三角形直接写出点P的坐标.
(3)将线段AB绕B点旋转90°,直接写出点A对应的点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年新型冠状病毒肺炎疫情肆虐,红星社区为了提高社区居民的身体素质,鼓励居民在家锻炼,特采购了一批跳绳免费发放,已知2根幸福牌跳绳和1根平安牌跳绳共需31元,2根平安牌跳绳和3根幸福牌跳绳共需54元.
(1)求幸福牌跳绳和平安牌跳绳的单价;
(2)已知该社区需要采购两种品牌的跳绳共60根,且平安牌跳绳的数量不少于幸福牌跳绳数量的2倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com