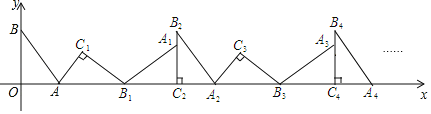
【题目】如图，在平面直角坐标系中，将△ABO绕点A顺指针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…，若点A（
，0）、B（0，4），则点B2020的横坐标为_____．
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案科目：初中数学 来源： 题型：
【题目】如图，已知等腰三角形ABC的底角为30°，以BC为直径的⊙O与底边AB交于点D，过D作DE⊥AC，垂足为E．
（1）证明：DE为⊙O的切线；
（2）连接OE，若BC=4，求△OEC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读：设试验结果落在某个区域S中每一点的机会均等，用A表示事件“试验结果落在S中的一个小区域M中”，那么事件A发生的概率P（A）
.在桌面上放一张50 cm×50 cm的正方形白纸ABCD，⊙O是它的内切圆，小明随机地将1000粒大米撒到该白纸上，其中落在圆内的大米有800粒，由此可得圆周率
的值为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学为了解七年级学生喜欢球类活动的情况，采取抽样调查的方法，从足球、乒乓球、篮球、排球等四个方面随机调查了部分七年级学生的兴趣爱好，根据调查的结果组建了
个兴趣小组，并绘制成如图所示的两幅不完整的统计图（如图①，②，要求每位学生只能选择一种自己喜欢的球类），请你根据图中提供的信息解答下列问题：
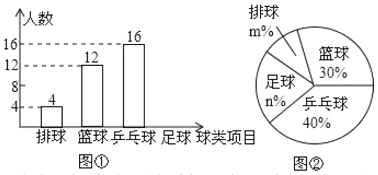
（1）求被抽查学生人数，将条形统计图补充完整；
（2）求出扇形统计图中，排球部分对应的圆心角度数；
（3）如果该中学七年级共有
名学生，请你估计七年级学生中喜欢排球的学生有多少名？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为更好开展“课后延时”服务，某校抽取了部分七年级学生，就课后活动项目进行调查．学校根据学生前期统计给出了如下四个选项：
“球类”、
“棋类”、
“计算机信息类”、
“其他”，并将最终调查结果绘制成如下两幅不完整的统计图．
根据图中提供的信息，解决下列问题：
(1)本次调查共抽取了____名学生，扇形统计图中，类所对应的扇形圆心角大小为
(2)将条形统计图补充完整；
(3)已知选择类的同学有两位来自七(1)班，其余来自七(2)班，调查组准备从选类同学中任选两位做细致分析求两位同学来自同一个班级的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
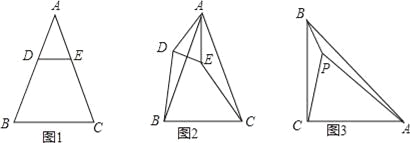
【题目】已知△ABC是等腰三角形，AB=AC．
（1）特殊情形：如图1，当DE∥BC时，有DB EC．（填“＞”，“＜”或“=”）
（2）发现探究：若将图1中的△ADE绕点A顺时针旋转α（0°＜α＜180°）到图2位置，则（1）中的结论还成立吗？若成立，请给予证明；若不成立，请说明理由．
（3）拓展运用：如图3，P是等腰直角三角形ABC内一点，∠ACB=90°，且PB=1，PC=2，PA=3，求∠BPC的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
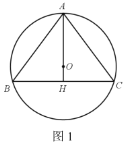
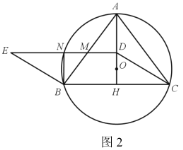
【题目】如图1，已知，⊙O是△ABC的外接圆，AB=AC=10，BC=12，连接AO并延长交BC于点H．
（1）求外接圆⊙O的半径；
（2）如图2，点D是AH上（不与点A，H重合）的动点，以CD，CB为边，作平行四边形CDEB，DE分别交⊙O于点N，交AB边于点M．
①连接BN，当BN⊥DE时，求AM的值；
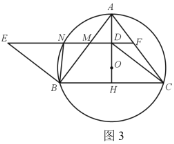
②如图3，延长ED交AC于点F，求证：NM·NF=AM·MB；
③设AM=x，要使
-2
<0成立，求x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市去年成功举办2018郴州国际休闲旅游文化节，获评“全国森林旅游示范市”．某市有A，B，C，D，E五个景区很受游客喜爱．一旅行社对某小区居民在暑假期间去以上五个景区旅游（只选一个景区）的意向做了一次随机调查统计，并根据这个统计结果制作了如下两幅不完整的统计图：
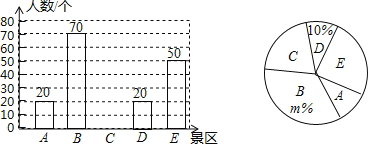
（1）该小区居民在这次随机调查中被调查到的人数是 人，
，并补全条形统计图；
（2）若该小区有居民1200人，试估计去B地旅游的居民约有多少人？
（3）小军同学已去过E地旅游，暑假期间计划与父母从A，B，C，D四个景区中，任选两个去旅游，求选到A，C两个景区的概率．（要求画树状图或列表求概率）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某超市销售一种商品，成本每千克40元，规定每千克售价不低于成本，且不高于80元，经市场调查，每天的销售量y（千克）与每千克售价x（元）满足一次函数关系，部分数据如下表：
售价x（元/千克） | 50 | 60 | 70 |
销售量y（千克） | 100 | 80 | 60 |
（1）求y与x之间的函数表达式；
（2）设商品每天的总利润为W（元），求W与x之间的函数表达式（利润＝收入﹣成本）；并求出售价为多少元时获得最大利润，最大利润是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
