Question

【题目】如图，已知等腰三角形ABC的底角为30°，以BC为直径的⊙O与底边AB交于点D，过D作DE⊥AC，垂足为E．

（1）证明：DE为⊙O的切线；

（2）连接OE，若BC=4，求△OEC的面积．

Answer 1

【答案】(1)证明见解析；（2）

【解析】试题分析：（1）首先连接OD，CD，由以BC为直径的⊙O，可得CD⊥AB，又由等腰三角形ABC的底角为30°，可得AD=BD，即可证得OD∥AC，继而可证得结论；

（2）首先根据三角函数的性质，求得BD，DE，AE的长，然后求得△BOD，△ODE，△ADE以及△ABC的面积，继而求得答案．

试题解析：（1）证明：连接OD，CD，

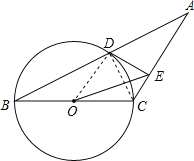
∵BC为⊙O直径，

∴∠BDC=90°，

即CD⊥AB，

∵△ABC是等腰三角形，

∴AD=BD，

∵OB=OC，

∴OD是△ABC的中位线，

∴OD∥AC，

∵DE⊥AC，

∴OD⊥DE，

∵D点在⊙O上，

∴DE为⊙O的切线；

（2）解：∵∠A=∠B=30°，BC=4，

∴CD=BC=2，BD=BCcos30°=2，

∴AD=BD=2，AB=2BD=4，

∴S△ABC=ABCD=×4×2=4，

∵DE⊥AC，

∴DE=AD=×2=，

AE=ADcos30°=3，

∴S△ODE=ODDE=×2×=，

S△ADE=AEDE=××3=，

∵S△BOD=S△BCD=×S△ABC=×4=，

∴S△OEC=S△ABC-S△BOD-S△ODE-S△ADE=4---=．