
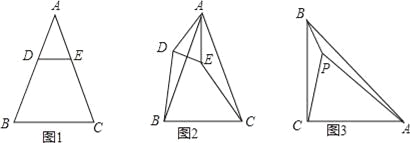
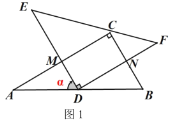
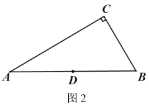
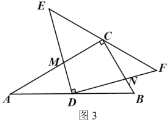
【题目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如图1,当DE∥BC时,有DB EC.(填“>”,“<”或“=”)
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.
【答案】(1)=;(2)成立,证明见解析;(3)135°.
【解析】
试题(1)由DE∥BC,得到![]() ,结合AB=AC,得到DB=EC;
,结合AB=AC,得到DB=EC;
(2)由旋转得到的结论判断出△DAB≌△EAC,得到DB=CE;
(3)由旋转构造出△CPB≌△CEA,再用勾股定理计算出PE,然后用勾股定理逆定理判断出△PEA是直角三角形,在简单计算即可.
试题解析:(1)∵DE∥BC,
∴![]() ,
,
∵AB=AC,
∴DB=EC,
故答案为=,
(2)成立.
证明:由①易知AD=AE,
∴由旋转性质可知∠DAB=∠EAC,
又∵AD=AE,AB=AC
∴△DAB≌△EAC,
∴DB=CE,
(3)如图,
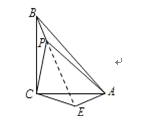
将△CPB绕点C旋转90°得△CEA,连接PE,
∴△CPB≌△CEA,
∴CE=CP=2,AE=BP=1,∠PCE=90°,
∴∠CEP=∠CPE=45°,
在Rt△PCE中,由勾股定理可得,PE=![]() ,
,
在△PEA中,PE2=(![]() )2=8,AE2=12=1,PA2=32=9,
)2=8,AE2=12=1,PA2=32=9,
∵PE2+AE2=AP2,
∴△PEA是直角三角形
∴∠PEA=90°,
∴∠CEA=135°,
又∵△CPB≌△CEA
∴∠BPC=∠CEA=135°.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
【题目】“一带一路”倡议提出五年多来,交通、通信、能源等各项相关建设取得积极进展,也为增进各国民众福祉提供了新的发展机遇.下图是2017年“一年一路”沿线部分国家的通信设施现状统计图.
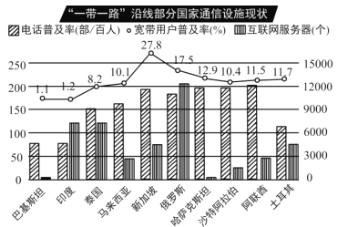
根据统计图提供的信息,下列推断合理的是( ).
A.互联网服务器拥有个数最多的国家是阿联酋
B.宽带用户普及率的中位数是11.05%
C.有8个国家的电话普及率能够达到平均每人1部
D.只有俄罗斯的三项指标均超过了相应的中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O及⊙O外一点P.
(1)方法证明:如何用直尺和圆规过点P作⊙O的一条切线呢?小明设计了如图①所示的方法:
①连接OP,以OP为直径作⊙O′;
②⊙O′与⊙O相交于点A,作直线PA.
则直线PA即为所作的过点P的⊙O的一条切线.
请证明小明作图方法的正确性.
(2)方法迁移:如图②,已知线段l,过点P作一条直线与⊙O相交,且该直线被⊙O所截得的弦长等于l.(保留作图痕迹,不要求写作法和证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
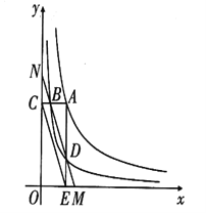
【题目】反比例函数![]() 在第一象限的图象如图所示,过
在第一象限的图象如图所示,过![]() 上任意一点
上任意一点![]() ,作
,作![]() 轴垂线交
轴垂线交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,作
,作![]() 轴垂线,交
轴垂线,交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于点
轴于点![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺指针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…,若点A(![]() ,0)、B(0,4),则点B2020的横坐标为_____.
,0)、B(0,4),则点B2020的横坐标为_____.
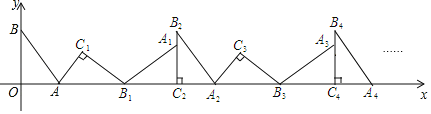
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在Rt△ABC和Rt△DEF中,∠ACB=∠EDF=90°,∠A=30°,∠E=45°,AB=EF=6,如图1,D是斜边AB的中点,将等腰Rt△DEF绕点D顺时针方向旋转角α(0°<α<90°),在旋转过程中,直线DE,AC相交于点M,直线DF,BC相交于点N.
(1)如图1,当α=60°时,求证:DM=BN;
(2)在上述旋转过程中,![]() 的值是一个定值吗?请在图2中画出图形并加以证明;
的值是一个定值吗?请在图2中画出图形并加以证明;
(3)如图3,在上述旋转过程中,当点C落在斜边EF上时,求两个三角形重合部分四边形CMDN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点A![]() 的直线l分别与x轴、y轴交于点C,D.
的直线l分别与x轴、y轴交于点C,D.
(1)求直线l的函数表达式.
(2)P为x轴上一点,若△PCD为等腰三角形直接写出点P的坐标.
(3)将线段AB绕B点旋转90°,直接写出点A对应的点A的坐标.
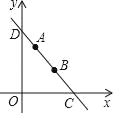
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=![]() (x>0)的图象上,则经过点B的反比例函数解析式为( )
(x>0)的图象上,则经过点B的反比例函数解析式为( )

A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象交反比例函数y=![]() (x>0)的图象于点A、B,交x轴于点C.
(x>0)的图象于点A、B,交x轴于点C.
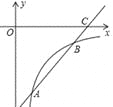
(1)求m的取值范围;
(2)若点A的坐标是(2,-4),且![]() =
=![]() ,求m的值和一次函数的解析式.
,求m的值和一次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com