
【题目】如图,已知一次函数y=kx+b的图象交反比例函数y=![]() (x>0)的图象于点A、B,交x轴于点C.
(x>0)的图象于点A、B,交x轴于点C.
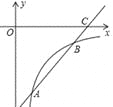
(1)求m的取值范围;
(2)若点A的坐标是(2,-4),且![]() =
=![]() ,求m的值和一次函数的解析式.
,求m的值和一次函数的解析式.
【答案】(1)m>2;(2)6,y=![]() x-5.
x-5.
【解析】
(1)根据反比例函数的图像位于第四象限即可得到关于m的不等式,解出即可;
(2)将A的坐标(2,-4)代入反比例解析式即可求得m的值,过AD⊥x轴,BE⊥x轴,证得△ECB∽△DCA,根据相似三角形的性质及![]() =
=![]() ,即可得到AD=4BE,由A(2,-4),即AD=4可得BE=1,再根据反比例函数的解析式即可求得点B的坐标,从而可以求得结果.
,即可得到AD=4BE,由A(2,-4),即AD=4可得BE=1,再根据反比例函数的解析式即可求得点B的坐标,从而可以求得结果.
(1)∵由于反比例函数的图像位于第四象限
∴4-2m<0,解得m>2;
(2)将A的坐标代入反比例解析式得:-4=![]() ,解得m=6
,解得m=6
作AD⊥x轴,BE⊥x轴,
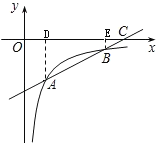
∵∠ADC=∠BEC=90°,∠ECB=∠DCA,
∴△ECB∽△DCA,
∵![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]()
∴AD=4BE,
又∵A(2,-4),即AD=4,
∴BE=1.
∵y=-![]() ,
,
将y=1代入反比例解析式,-1=-![]() ,即x=8,
,即x=8,
∴B(8,-1).
将A(2,-4),B(8,-1)代入一次函数解析式,
得![]() ,解得:
,解得: .
.
∴y=![]() x-5.
x-5.


科目:初中数学 来源: 题型:
【题目】已知△ABC是等腰三角形,AB=AC.
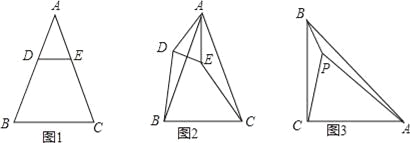
(1)特殊情形:如图1,当DE∥BC时,有DB EC.(填“>”,“<”或“=”)
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:y=k1x+b过A(0,﹣3),B(5,2),直线l2:y=k2x+2.
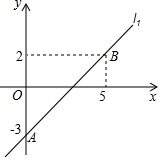
(1)求直线l1的表达式;
(2)当x≥4时,不等式k1x+b>k2x+2恒成立,请写出一个满足题意的k2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本);并求出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,延长
,延长![]() 交
交![]() 于G,
于G,![]() ,垂足为H,连接
,垂足为H,连接![]() ,.以下结论:①
,.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中正确的个数是()
;其中正确的个数是()
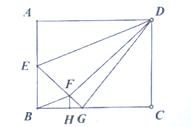
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步深化基教育课程改革,构建符合素质教育要求的学校课程体系,某学校自主开发了A书法、B阅读,C足球,D器乐四门校本选修课程供学生选择,每门课程被选到的机会均等.
(1)学生小红计划选修两门课程,请写出所有可能的选法;
(2)若学生小明和小刚各计划送修一门课程,则他们两人恰好选修同一门课程的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 中,
中,![]() ,B是边AD上一点,以AB为直径的
,B是边AD上一点,以AB为直径的![]() 经过点P,C是
经过点P,C是![]() 上一动点,连接AC,PC,PC交AB于点E,且
上一动点,连接AC,PC,PC交AB于点E,且![]() .
.
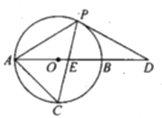
(1)求证:PD是![]() 的切线;
的切线;
(2)连接OP,PB,BC,OC,若![]() 的直径是4,则:
的直径是4,则:
①当四边形APBC是矩形时,求DE的长;
②当![]() ______时,四边形OPBC是菱形.
______时,四边形OPBC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴快车是一种便捷的出行工具,计价规则如下表:
计费项目 | 里程费 | 时长费 | 远途费 |
单价 | 1.8元/千米 | 0.3元/分 | 0.8元/千米 |
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为行车里程7千米以内(含7千米)不收远途费,超过7千米的,超出部分每千米收0.8元. | |||
(1)小王与小张各自乘坐滴滴快车,在同一地点约见,已知到达约见地点,他们的实际行车里程分别为6千米与8.5千米,两人付给滴滴快车的乘车费相同(1)求这两辆滴滴快车的实际行车时间相差多少分钟;
(2)实际乘车时间较少的人,由于出发时间比另一人早,所以提前到达约见地点在大厅等候.已知他等候另一人的时间是他自己实际乘车时间的1.5倍,且比另一人的实际乘车时间的一半多8.5分钟,计算两人各自的实际乘车时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com