练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】滴滴快车是一种便捷的出行工具，计价规则如下表：

    计费项目

    里程费

    时长费

    远途费

    单价

    1.8元/千米

    0.3元/分

    0.8元/千米

    注：车费由里程费、时长费、远途费三部分构成，其中里程费按行车的实际里程计算；时长费按行车的实际时间计算；远途费的收取方式为行车里程7千米以内（含7千米）不收远途费，超过7千米的，超出部分每千米收0.8元.

    （1）小王与小张各自乘坐滴滴快车，在同一地点约见，已知到达约见地点，他们的实际行车里程分别为6千米与8.5千米，两人付给滴滴快车的乘车费相同（1）求这两辆滴滴快车的实际行车时间相差多少分钟；

    （2）实际乘车时间较少的人，由于出发时间比另一人早，所以提前到达约见地点在大厅等候.已知他等候另一人的时间是他自己实际乘车时间的1.5倍，且比另一人的实际乘车时间的一半多8.5分钟，计算两人各自的实际乘车时间.

    【答案】（1）这两辆滴滴快车的实际行车时间相差19分钟.（2）小王的实际乘车时间为37分钟，小张的实际乘车时间为18分钟.

    【解析】

    (1)设小王实际乘车时间为x分钟,小张乘车时间为y分钟,由题意列出方程解出关系式即可.

    (2)由题意列出方程,再与(1)中关系式组合成方程组,解出即可.

    （1）设小王乘坐的滴滴快车的实际行车时间为x分钟，

    小张乘坐的滴滴快车的实际行车时间为y分钟.

    由题意，得

    ，

    ，

    .

    答：这两辆滴滴快车的实际行车时间相差19分钟.

    （2）由（1）及题意，得，

    化简得

    得，

    解得.③

    将③代入①，得.

    答：小王的实际乘车时间为37分钟，小张的实际乘车时间为18分钟.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地，行驶过程中的函数图像如图所示。

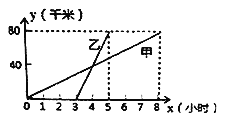
    （1）请根据图像回答下列问题：甲先出发 小时后，乙才出发；在甲出发 小时后两人相遇，这时他们距A地 千米；

    （2）乙的行驶速度 千米/小时；

    （3）分别求出甲、乙在行驶过程中的路程（千米）与时间（小时）之间的函数关系式（不要求写出自变量的取值范围）。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

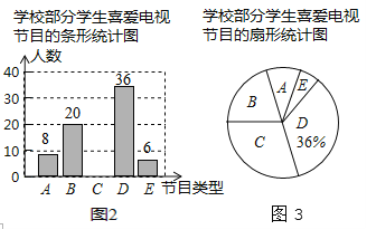
    【题目】为了了解本校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，课题小组随机选取该校部分学生进行了问卷调査（问卷调査表如图1所示），并根据调查结果绘制了图2、图3两幅统计图（均不完整），请根据统计图解答下列问题．

    （1）本次接受问卷调查的学生有________名．

    （2）补全条形统计图．

    （3）扇形统计图中B类节目对应扇形的圆心角的度数为________．

    （4）该校共有2000名学生，根据调查结果估计该校最喜爱新闻节目的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两船从同一个港口同时出发反向而行，甲船顺水航行了6小时，乙船逆水行了3小时，两船在静水中的速度都是50 km/h，水流速度是a km/h

    (1) 两船一共航行了多少千米

    (2) 甲船比乙船多航行多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校七年级1至4班计划每班购买数量相同的图书布置班级读书角，但是由于种种原因，实际购书量与计划有出入，下表是实际购书情况：

    班级

    1班

    2班

    3班

    4班

    实际购买量（本）

    a

    33

    c

    21

    实际购买量与计划购数量的差值（本）

    ＋12

    b

    －8

    －9

    (1) 直接写出a＝__________，b＝__________，c＝__________

    (2) 根据记录的数据可知4个班实际购书共_________本

    (3) 书店给出一种优惠方案：一次购买不少于15本，其中2本书免费．若每本书售价为30元，请计算这4个班整体购书的最低总花费是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】是某汽车行驶的路程S(km)与时间t(min)的函数关系图．观察图中所提供的信息，解答下列问题：

    （1）汽车在前9分钟内的平均速度是多少？

    （2）汽车在中途停了多长时间？

    （3）当16≤t≤30时，求S与t的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知是由经过平移得到的，其中A，B，C三点的对应点分别是，，，它们在平面直角坐标系中的坐标如下表所示：

    （1）观察表中各对应点坐标的变化，并填空：__________，__________．

    （2）在下图的平面直角坐标系中画出和．

    （3）写出是怎样平移得到的？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣4，3），B（﹣3，1），C（﹣1，3）．

    （1）请按下列要求画图：

    ①平移△ABC，使点A的对应点A1的坐标为（﹣4，﹣3），请画出平移后的△A1B1C1；

    ②△A2B2C2与△ABC关于原点O中心对称，画出△A2B2C2．

    （2）若将△A1B1C1绕点M旋转可得到△A2B2C2，请直接写出旋转中心M点的坐标　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y＝x －2mx(m为常数)，当－1≤x≤2时，函数y的最小值为－2，则m的值是(　　)

    A. B. C. 或 D. －或

    查看答案和解析>>

    同步练习册答案