
����Ŀ����֪��O����O��һ��P��
��1������֤���������ֱ�ߺ�Բ�����P����O��һ�������أ�С���������ͼ����ʾ�ķ�����
������OP����OPΪֱ������O����
�ڡ�O�����O�ཻ�ڵ�A����ֱ��PA��
��ֱ��PA��Ϊ�����Ĺ���P�ġ�O��һ�����ߣ�
��֤��С����ͼ��������ȷ�ԣ�
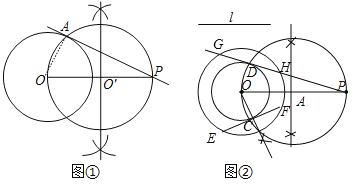
��2������Ǩ�ƣ���ͼ�ڣ���֪�߶�l������P��һ��ֱ�����O�ཻ���Ҹ�ֱ�߱���O���صõ��ҳ�����l����������ͼ�ۼ�����Ҫ��д������֤����

���𰸡���1������������2��������
��������
��1������OA��ֻҪ֤��OA��PA���ɣ�
��2���ڴ�Բ��O��ȡ��E����ȡEF=�߶�l������Բ��O�ڵ�F����EF�Ĵ�ֱƽ����OC������ΪC���Ե�OΪԲ�ģ�OCΪ�뾶��СԲ��O������OP����OPΪֱ����Բ��A����СԲ��O�ڵ�D������OD��PD���ӳ���Q�����Բ��O���ڵ�G��H����OD��PD������ΪD����OD=OC���ɵ�GH=EF=�߶�l��
��1��֤������ͼ���У�����OA��
��OP��ֱ����
���OAP=90����
��OA��PA��
��PA����O�����ߣ�
��2���⣺�������ڴ�Բ��O��ȡ��E����ȡEF=�߶�l������Բ��O�ڵ�F��
��EF�Ĵ�ֱƽ����OC������ΪC��
�Ե�OΪԲ�ģ�OCΪ�뾶��СԲ��O��
����OP����OPΪֱ����Բ��A��
��СԲ��O�ڵ�D��
����OD��PD���ӳ���Q�����Բ��O���ڵ�G��H��
��ΪOP����A��ֱ����
������PDO=90������OD��PD������ΪD��
��OD=OC��
��GH=EF=�߶�l��


 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
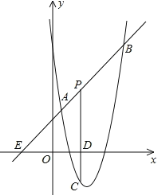
����Ŀ����ͼ��ֱ��y=x+2��������y=ax2+bx+6��a��0���ཻ��A��![]() ��
��![]() ����B��4��m������P���߶�AB������A��B�Ķ��㣬����P��PC��x���ڵ�D�����������ڵ�C��
����B��4��m������P���߶�AB������A��B�Ķ��㣬����P��PC��x���ڵ�D�����������ڵ�C��
��1���������ߵĽ���ʽ��
��2���Ƿ����������P�㣬ʹ�߶�PC�ij������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
��3��������PACΪֱ�������Σ�ֱ��д����P���ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����y![]() ��x��0����ͼ����ֱ��y=2x+1���ڵ�A��1��m��
��x��0����ͼ����ֱ��y=2x+1���ڵ�A��1��m��
��1����k��m��ֵ��
��2����֪��P��0��n����n��0��������P��ƽ����x���ֱ�ߣ���ֱ��y=2x+1�ڵ�B��������y![]() ��x��0����ͼ���ڵ�C���ᡢ�����궼�������ĵ�������㣮
��x��0����ͼ���ڵ�C���ᡢ�����궼�������ĵ�������㣮
����n=1ʱ��д���߶�BC�ϵ���������ꣻ
����y![]() ��x��0����ͼ���ڵ�A��C֮��IJ������߶�AB��BC��Χ�ɵ������ڣ������߽磩ǡ��6�����㣬ֱ��д��n��ȡֵ��Χ��
��x��0����ͼ���ڵ�A��C֮��IJ������߶�AB��BC��Χ�ɵ������ڣ������߽磩ǡ��6�����㣬ֱ��д��n��ȡֵ��Χ��
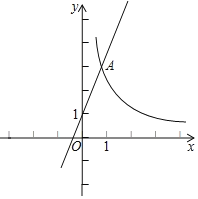
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() �ύ��
�ύ��![]() ����(��
����(��![]() �ڵ�
�ڵ�![]() ���)����
���)����![]() �ύ�ڵ�
�ύ�ڵ�![]() �����Ϊ
�����Ϊ![]() ������
������![]() �ӵ�
�ӵ�![]() ������
������![]() ������ÿ��
������ÿ��![]() ����λ���ٶ����
����λ���ٶ����![]() �˶�����
�˶�����![]() ��
��![]() �ύ
�ύ![]() ��
��![]() ������������
������������![]() ��
��

![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
![]() ��
��![]() ���ʱ�����˶���ʱ�䣮
���ʱ�����˶���ʱ�䣮
![]() �����ʱ�䣬��
�����ʱ�䣬��![]() ����
����![]() ����
����![]() �ľ�����ȣ�
�ľ�����ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ���������������ij������S��ÿһ��Ļ�����ȣ���A��ʾ�¼�������������S�е�һ��С����M��������ô�¼�A�����ĸ���P��A��![]() .�������Ϸ�һ��50 cm��50 cm�������ΰ�ֽABCD����O����������Բ��С������ؽ�1000�����������ð�ֽ�ϣ���������Բ�ڵĴ�����800�����ɴ˿ɵ�Բ����
.�������Ϸ�һ��50 cm��50 cm�������ΰ�ֽABCD����O����������Բ��С������ؽ�1000�����������ð�ֽ�ϣ���������Բ�ڵĴ�����800�����ɴ˿ɵ�Բ����![]() ��ֵΪ�� ��
��ֵΪ�� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
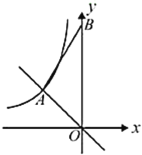
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]()
![]() ��ͼ����
��ͼ����![]() �㣬��
�㣬��![]() Ϊ
Ϊ![]() ����������һ�㣬��
����������һ�㣬��![]() ��
��![]() �������
�������![]() ����
����![]() _______��
_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ�˽����꼶ѧ��ϲ���������������ȡ��������ķ�����������ƹ��������������ĸ�������������˲������꼶ѧ������Ȥ���ã����ݵ���Ľ���齨��![]() ����ȤС�飬�����Ƴ���ͼ��ʾ��������������ͳ��ͼ����ͼ�٣��ڣ�Ҫ��ÿλѧ��ֻ��ѡ��һ���Լ�ϲ�������ࣩ���������ͼ���ṩ����Ϣ����������⣺
����ȤС�飬�����Ƴ���ͼ��ʾ��������������ͳ��ͼ����ͼ�٣��ڣ�Ҫ��ÿλѧ��ֻ��ѡ��һ���Լ�ϲ�������ࣩ���������ͼ���ṩ����Ϣ����������⣺
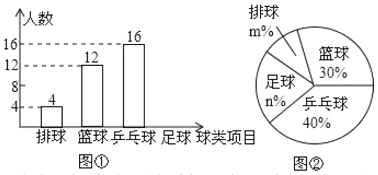
��1�����ѧ��������������ͳ��ͼ����������
��2���������ͳ��ͼ�У����ֶ�Ӧ��Բ�ĽǶ�����
��3���������ѧ���꼶����![]() ��ѧ��������������꼶ѧ����ϲ�������ѧ���ж�������
��ѧ��������������꼶ѧ����ϲ�������ѧ���ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
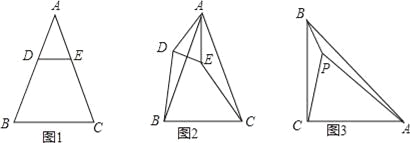
����Ŀ����֪��ABC�ǵ��������Σ�AB=AC��
��1���������Σ���ͼ1����DE��BCʱ����DB EC������������������������=����
��2������̽��������ͼ1�е���ADE�Ƶ�A˳ʱ����ת����0��������180������ͼ2λ�ã���1���еĽ��ۻ��������������������֤����������������˵�����ɣ�
��3����չ���ã���ͼ3��P�ǵ���ֱ��������ABC��һ�㣬��ACB=90������PB=1��PC=2��PA=3������BPC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��l1��y��k1x+b��A��0����3����B��5��2����ֱ��l2��y��k2x+2��
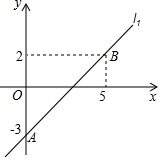
��1����ֱ��l1�ı���ʽ��
��2����x��4ʱ������ʽk1x+b��k2x+2���������д��һ�����������k2��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com