
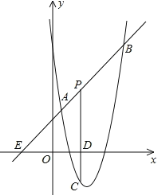
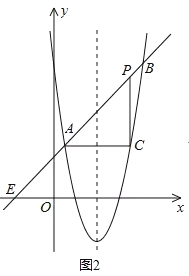
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(![]() ,
,![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)假若△PAC为直角三角形,直接写出点P坐标。
【答案】(1)y=2x2-8x+6(2)存在,![]() (3)(3,5)
(3)(3,5)
【解析】
(1)已知B(4,m)在直线y=x+2上,可求得m的值,抛物线图象上的A、B两点坐标,可将其代入抛物线的解析式中,通过待定系数法即可求得解析式;
(2)设出P点横坐标,根据直线AB和抛物线的解析式表示出P、C的纵坐标,进而得到关于PC与P点横坐标的函数关系式,化成顶点式即可;
(3)当△PAC为直角三角形时,根据直角顶点的不同,有三种情形,需要分类讨论,分别求解.
(1)∵B(4,m)在直线y=x+2上,
∴m=4+2=6,
∴B(4,6),
∵A(![]() ,
,![]() ),B(4,6)在抛物线y=ax2+bx+6上,
),B(4,6)在抛物线y=ax2+bx+6上,
∴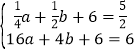 ,
,
解得![]() ,
,
∴抛物线的解析式为y=2x28x+6;
(2)设动点P的坐标为(n,n+2),则C点的坐标为(n,2n28n+6),
∴PC=(n+2)(2n28n+6)=2n2+9n4=2(n![]() )2+
)2+![]() ,
,
∵PC>0,
∴当n=![]() 时,线段PC最大且为
时,线段PC最大且为![]() ;
;
(3)∵△PAC为直角三角形,
i)若点P为直角顶点,则∠APC=90°.
由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;
ii)若点A为直角顶点,则∠PAC=90°.
如图1,
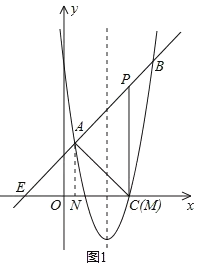
过点A(![]() ,
,![]() )作AN⊥x轴于点N,则ON=
)作AN⊥x轴于点N,则ON=![]() ,AN=
,AN=![]() ,
,
过点A作AM⊥直线AB,交x轴于点M,
则由题意易知,△AMN为等腰直角三角形,
∴MN=AN=![]() ,
,
∴OM=ON+MN=![]() +
+![]() =3,
=3,
∴M(3,0).
设直线AM的解析式为:y=kx+b,
则: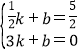 ,
,
解得![]() ,
,
∴直线AM的解析式为:y=x+3 ①
又抛物线的解析式为:y=2x28x+6 ②
联立①②式,解得:x=3或x=![]() (与点A重合,舍去)
(与点A重合,舍去)
∴C(3,0),即点C、M点重合;
当x=3时,y=x+2=5,
∴P1(3,5);
iii)若点C为直角顶点,则∠ACP=90°.
∵y=2x28x+6=2(x2)22,
∴抛物线的对称轴为直线x=2.
如图2,作点A(![]() ,
,![]() ))关于对称轴x=2的对称点C,
))关于对称轴x=2的对称点C,
则点C在抛物线上,且C(![]() ,
,![]() ),
),
当x=![]() 时,y=x+2=
时,y=x+2=![]() ,
,
∴P2(![]() ,
,![]() ).
).
∵点P1(3,5)、P2(![]() ,
,![]() )均在线段AB上,
)均在线段AB上,
∴综上所述,△PAC为直角三角形时,点P的坐标为(3,5)或(![]() ,
,![]() ).
).


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 如果一件事不可能发生,那么它是必然事件,即发生的概率是![]()
B. 不太可能发生的事情的概率不为![]()
C. 若一件事情肯定发生,则其发生的概率![]()
D. 概率很大的事情必然发生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线l的解析式为:y=kx+x﹣k+1,若将直线l绕A点旋转.如图所示,当直线l旋转到l1位置时,k=2且l1与y轴交于点B,与x轴交于点C;当直线l旋转到l2位置时,k=﹣![]() 且l2与y轴交于点D
且l2与y轴交于点D
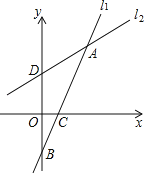
(1)求点A的坐标;
(2)直接写出B、C、D三点的坐标,连接CD计算△ADC的面积;
(3)已知坐标平面内一点E,其坐标满足条件E(a,a),当点E与点A距离最小时,直接写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c经过矩形ABCD的两个顶点A、B,AB平行于x轴,对角线BD与抛物线交于点P,点A的坐标为(0,2),AB=4.
(1)求抛物线的解析式;
(2)若S△APO=![]() ,求矩形ABCD的面积.
,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,AB=AC,点D 在底边BC 上,AE=AD,连接 DE.
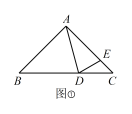
(1)如图①,已知∠BAC=90°,∠BAD=60°,求 ∠CDE 的度数;
(2)如图①,已知∠BAC=90°,当点D 在线段BC(点B,C 除外)上运动时,试探究∠BAD与 ∠CDE 的数量关系;
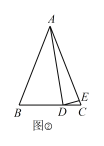
(3)如图②,若 ∠BAC≠90°,试探究∠BAD与 ∠CDE 的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,学校准备在教师周转房旁边搭建一个简易矩形摩托车车棚,一边利用教学楼的后墙(可利用的墙长为19m),另外三边利用学校现有总长38m的铁栏围成.
(1)若围成的面积为180m2,试求出摩托车车棚的长和宽;
(2)能围成的面积为200m2摩托车车棚吗?如果能,请你给出设计方案;如果不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图(1),在平面直角坐标系中,点A、点B分別在x轴、y轴的正半轴上,点C在第一象限,∠ACB=90°,AC=BC,点A坐标为(m,0),点C横坐标为n,且m2+n2﹣2m﹣8n+17=0.
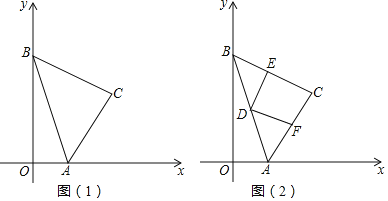
(1)分別求出点A、点B、点C的坐标;
(2)如图(2),点D为边AB中点,以点D为顶点的直角∠EDF两边分别交边BC于E,交边AC于F,①求证:DE=DF;②求证:S四边形DECF=![]() S△ABC;
S△ABC;
(3)在坐标平面内有点G(点G不与点A重合),使得△BCG是以BC为直角边的等腰直角三角形,请直接写出满足条件的点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是黄金分割比(黄金分割比0.618)著名的“断臂维纳斯”便是如此.此外最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是黄金分割比.若某人满足上述两个黄金分割比例,且腿长为103cm,头顶至脖子下端的长度为25cm,则其身高可能是( )

A.165cmB.170cmC.175cmD.180cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com