
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊжБЯпlЕФНтЮіЪНЮЊЃКyЃНkx+xЉk+1ЃЌШєНЋжБЯпlШЦAЕуа§зЊЃЎШчЭМЫљЪОЃЌЕБжБЯпlа§зЊЕНl1ЮЛжУЪБЃЌkЃН2Чвl1гыyжсНЛгкЕуBЃЌгыxжсНЛгкЕуCЃЛЕБжБЯпlа§зЊЕНl2ЮЛжУЪБЃЌkЃНЉ![]() Чвl2гыyжсНЛгкЕуD
Чвl2гыyжсНЛгкЕуD
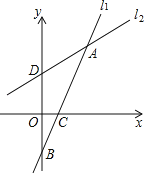
ЃЈ1ЃЉЧѓЕуAЕФзјБъЃЛ
ЃЈ2ЃЉжБНгаДГіBЁЂCЁЂDШ§ЕуЕФзјБъЃЌСЌНгCDМЦЫуЁїADCЕФУцЛ§ЃЛ
ЃЈ3ЃЉвбжЊзјБъЦНУцФквЛЕуEЃЌЦфзјБъТњзуЬѕМўEЃЈaЃЌaЃЉЃЌЕБЕуEгыЕуAОрРызюаЁЪБЃЌжБНгаДГіaЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉAЕуЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЃЛЃЈ2ЃЉBЃЈ0ЃЌЉ1ЃЉЁЂCЃЈ![]() ЃЌ0ЃЉЁЂDЃЈ0ЃЌ
ЃЌ0ЃЉЁЂDЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ![]() ЃЛЃЈ3ЃЉaЃН
ЃЛЃЈ3ЃЉaЃН![]()
ЁОНтЮіЁП
ЃЈ1ЃЉНЋkЃН2КЭkЃН![]() ДњШыжБЯпЕФНтЮіЪНЃЌЕУЕНЙигкxЁЂyЕФЗНГЬзщЃЌШЛКѓНтЗНГЬзщПЩЧѓЕУЕуAЕФзјБъЃЛ
ДњШыжБЯпЕФНтЮіЪНЃЌЕУЕНЙигкxЁЂyЕФЗНГЬзщЃЌШЛКѓНтЗНГЬзщПЩЧѓЕУЕуAЕФзјБъЃЛ
ЃЈ2ЃЉСЌНгDCЃЎЯШЧѓЕУЕуBЁЂCЁЂDЕФзјБъЃЌШЛКѓвРОнSЁїADCЃНSЁїADBЉSЁїBDCЧѓНтМДПЩЃЛ
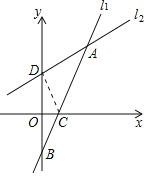
ЃЈ3ЃЉЙ§ЕуAзїжБЯпyЃНxЕФДЙЯпЃЌДЙзуЮЊEЃЌЙ§ЕуAзїAFЁЮyжсЃЌЙ§ЕуEзїEGЁЭAFЃЌДЙзуЮЊGЃЎЯШЧѓЕУAFЕФжЕЃЌШЛКѓгЩЁїAEFЮЊЕШбќжБНЧШ§НЧаЮЃЌДгЖјПЩЧѓЕУЕуEЕФзјБъЃЌЙЪДЫПЩЕУЕНaЕФжЕЃЎ
ЃЈ1ЃЉЕБkЃН2ЪБЃЌyЃН3xЉ1ЃЌ
ЕБkЃНЉ![]() ЪБЃЌyЃН
ЪБЃЌyЃН![]() x+
x+![]() ЃЎ
ЃЎ
НтЗНГЬзщЃЌ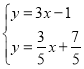
ЕУЃК![]() ЃЌ
ЃЌ
ЁрAЕуЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЃЎ
ЃЈ2ЃЉСЌНгDCЃЎ
НЋxЃН0ДњШыyЃН3xЉ1ЕУЃКyЃНЉ1ЃЌ
ЁрBЃЈ0ЃЌЉ1ЃЉЃЎ
НЋyЃН0ДњШыyЃН3xЉ1ЕУЃК3xЉ1ЃН0ЃЌНтЕУЃКxЃН![]() ЃЎ
ЃЎ
ЁрCЃЈ![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ
НЋxЃН0ДњШыyЃН![]() x+
x+![]() ЕУЃКyЃН
ЕУЃКyЃН![]() ЃЌ
ЃЌ
ЁрDЃЈ0ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁрBDЃН![]() ЃЌOCЃН
ЃЌOCЃН![]() ЃЎ
ЃЎ
ЁрSЁїADCЃНSЁїADBЉSЁїBDCЃН![]() ЁС
ЁС![]() ЁС1Љ
ЁС1Љ![]() ЁС
ЁС![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЁпEЃЈaЃЌaЃЉЃЌ
ЁрЕуEдкжБЯпyЃНxЩЯЃЎ
ШчЭМЫљЪОЃКЙ§ЕуAзїжБЯпyЃНxЕФДЙЯпЃЌДЙзуЮЊEЃЌЙ§ЕуAзїAFЁЮyжсЃЌЙ§ЕуEзїEGЁЭAFЃЌДЙзуЮЊGЃЎ
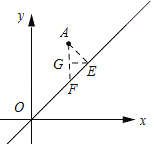
НЋxЃН1ДњШыyЃНxЕУЃКyЃН1ЃЌ
ЁрAFЃН2Љ1ЃН1ЃЎ
ЁпЕуEдкжБЯпyЃНxЩЯЃЌ
ЁрЁЯAFEЃН45ЁуЃЌ
ЁрЁїAEFЮЊЕШбќжБНЧШ§НЧаЮЃЎ
ЁпEGЁЭAFЃЌ
ЁрAGЃНFGЃН![]() ЃЌ
ЃЌ
ЁрEЕФзнзјБъЃН1+![]() ЃН
ЃН![]() ЃЎ
ЃЎ
ЁрaЃН![]() ЃЎ
ЃЎ


 аЁбЇЩњ10ЗжжгПкЫуВтЪд100ЗжЯЕСаД№АИ
аЁбЇЩњ10ЗжжгПкЫуВтЪд100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
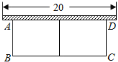
ЁОЬтФПЁПШчЭМЃЌгаГЄЮЊ![]() ЕФРщАЪЃЌвЛУцРћгУЧНЃЈЧНЕФзюДѓПЩгУГЄЖШЮЊ
ЕФРщАЪЃЌвЛУцРћгУЧНЃЈЧНЕФзюДѓПЩгУГЄЖШЮЊ![]() ЃЉЃЌЮЇГЩжаМфИєгавЛЕРРщАЪЃЈЦНаагк
ЃЉЃЌЮЇГЩжаМфИєгавЛЕРРщАЪЃЈЦНаагк![]() ЃЉЕФОиаЮЛЈЦд
ЃЉЕФОиаЮЛЈЦд![]() ЃЎЩшЛЈЦдЕФвЛБп
ЃЎЩшЛЈЦдЕФвЛБп![]() ЮЊ
ЮЊ![]() ЃЎ
ЃЎ
![]() дђ
дђ![]() ________ЃЈгУКЌ
________ЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉЃЌОиаЮ
ЕФДњЪ§ЪНБэЪОЃЉЃЌОиаЮ![]() ЕФУцЛ§
ЕФУцЛ§![]() ________ЃЈгУКЌ
________ЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЕФДњЪ§ЪНБэЪОЃЉЃЛ
![]() ШчЙћвЊЮЇГЩУцЛ§ЮЊ
ШчЙћвЊЮЇГЩУцЛ§ЮЊ![]() ЕФЛЈЦдЃЌ
ЕФЛЈЦдЃЌ![]() ЕФГЄЪЧЖрЩйЃП
ЕФГЄЪЧЖрЩйЃП
![]() НЋ
НЋ![]() жаБэЪООиаЮ
жаБэЪООиаЮ![]() ЕФУцЛ§ЕФДњЪ§ЪНЭЈЙ§ХфЗНЃЌЮЪЃКЕБ
ЕФУцЛ§ЕФДњЪ§ЪНЭЈЙ§ХфЗНЃЌЮЪЃКЕБ![]() ЕШгкЖрЩйЪБЃЌФмЙЛЪЙОиаЮЛЈЦд
ЕШгкЖрЩйЪБЃЌФмЙЛЪЙОиаЮЛЈЦд![]() УцЛ§зюДѓЃЌзюДѓЕФУцЛ§ЮЊЖрЩйЃП
УцЛ§зюДѓЃЌзюДѓЕФУцЛ§ЮЊЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЬНОПШ§НЧаЮЕФФкНЧКЭЕФаЁзщЛюЖЏжаЃЌаЁгБзїШчЯТИЈжњЯпЃКбгГЄЁїABCЕФБпBCЕНDЃЌзїCEЁЮABЃЌгкЪЧаЁгБЕУГіШ§НЧаЮФкНЧКЭЕФжЄУїЗНЗЈЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯA+ЁЯB+ЁЯACBЃН180ЁуЃЛ
ЃЈ2ЃЉШчЙћCEЦНЗжЁЯACDЃЌACЃН5ЃЌЧѓBCЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌADЪЧЁїABCЕФНЧЦНЗжЯпЃЌDFЁЭABЃЌДЙзуЮЊFЃЌDEЃНDGЃЌЁїADGКЭЁїAEDЕФУцЛ§ЗжБ№ЮЊ40КЭ28ЃЌдђЁїEDFЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ

A. 12 B. 6 C. 7 D. 8
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
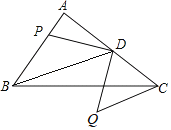
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯAЃН90ЁуЃЌABЃН4ЃЌACЃН6ЃЌЕуDЮЊACжаЕуЃЌЕуPЮЊABЩЯЕФЖЏЕуЃЌНЋЕуPШЦЕуDФцЪБеыа§зЊ90ЁуЕУЕНЕуQЃЌСЌНгCQЃЌдђЯпЖЮCQЕФзюаЁжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() ЁЂ
ЁЂ![]() ЦНЗжЯпЕФНЛЕуЃЌЧв
ЦНЗжЯпЕФНЛЕуЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌдђЕу
ЃЌдђЕу![]() ЕНБп
ЕНБп![]() ЕФОрРыЮЊЃЈ ЃЉ
ЕФОрРыЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
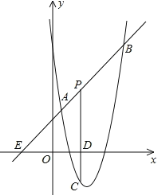
ЁОЬтФПЁПШчЭМЃЌжБЯпy=x+2гыХзЮяЯпy=ax2+bx+6ЃЈaЁй0ЃЉЯрНЛгкAЃЈ![]() ЃЌ
ЃЌ![]() ЃЉКЭBЃЈ4ЃЌmЃЉЃЌЕуPЪЧЯпЖЮABЩЯвьгкAЁЂBЕФЖЏЕуЃЌЙ§ЕуPзїPCЁЭxжсгкЕуDЃЌНЛХзЮяЯпгкЕуCЃЎ
ЃЉКЭBЃЈ4ЃЌmЃЉЃЌЕуPЪЧЯпЖЮABЩЯвьгкAЁЂBЕФЖЏЕуЃЌЙ§ЕуPзїPCЁЭxжсгкЕуDЃЌНЛХзЮяЯпгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЪЧЗёДцдкетбљЕФPЕуЃЌЪЙЯпЖЮPCЕФГЄгазюДѓжЕЃПШєДцдкЃЌЧѓГіетИізюДѓжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉМйШєЁїPACЮЊжБНЧШ§НЧаЮЃЌжБНгаДГіЕуPзјБъЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
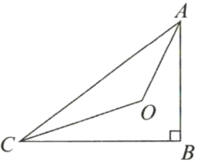
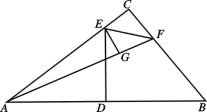
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯCЃН90ЁуЃЌABЕФДЙжБЦНЗжЯпDEНЛACгкЕуEЃЌДЙзуЪЧDЃЌFЪЧBCЩЯвЛЕуЃЌEFЦНЗжЁЯAFCЃЌEGЁЭAFгкЕуGЃЎ
ЃЈ1ЃЉЪдХаЖЯECгыEGЃЌCFгыGFЪЧЗёЯрЕШЃЛЃЈжБНгаДГіНсЙћЃЌВЛвЊЧѓжЄУїЃЉ
ЃЈ2ЃЉЧѓжЄЃКAGЃНBCЃЛ
ЃЈ3ЃЉШєABЃН5ЃЌAF+BFЃН6ЃЌЧѓEGЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЃКABЮЊЁбOЕФЯвЃЈЗЧжБОЖЃЉЃЌEЮЊABЕФжаЕуЃЌEOЕФбгГЄЯпгыЁбOЯрНЛгкCЃЌCMЁЮABЃЌBOЕФбгГЄЯпгыЁбOЯрНЛгкFЃЌгыCMЯрНЛгкDЃЎ
ЂйЧѓжЄЃКECЁЭCDЃЛ
ЂкЕБEOЃКOC=1ЃК3ЃЌCD=4ЪБЃЌЧѓЁбOЕФАыОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com