【题目】如图所示，学校准备在教师周转房旁边搭建一个简易矩形摩托车车棚，一边利用教学楼的后墙（可利用的墙长为19m），另外三边利用学校现有总长38m的铁栏围成．
（1）若围成的面积为180m2，试求出摩托车车棚的长和宽；
（2）能围成的面积为200m2摩托车车棚吗？如果能，请你给出设计方案；如果不能，请说明理由．
【答案】摩托车棚长19m，宽10m.
【解析】
（1）利用长方形的周长表示出各边长，即可表示出矩形面积，求出即可；
（2）利用长方形的面积列方程，利用根的判别式解答即可．
(1)设AB=x，则BC=382x；
根据题意列方程的，
x(382x)=180，
解得x1=10,x2=9；
当x=10,382x=18(米)，
当x=9,382x=20(米)，而墙长19m，不合题意舍去，
答：若围成的面积为180m2，自行车车棚的长和宽分别为10米，18米；
(2)根据题意列方程的，
x(382x)=200，
整理得出：x219x+100=0；
△=b24ac=361400=39<0，
故此方程没有实数根，
答：因此如果墙长19m,满足条件的花园面积不能达到200m2.
夺冠金卷全能练考系列答案科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中（如图）．已知抛物线y=﹣
x2+bx+c经过点A（﹣1，0）和点B（0，
），顶点为C，点D在其对称轴上且位于点C下方，将线段DC绕点D按顺时针方向旋转90°，点C落在抛物线上的点P处．
（1）求这条抛物线的表达式；
（2）求线段CD的长；
（3）将抛物线平移，使其顶点C移到原点O的位置，这时点P落在点E的位置，如果点M在y轴上，且以O、D、E、M为顶点的四边形面积为8，求点M的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
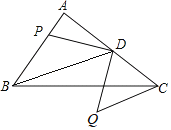
【题目】如图，在Rt△ABC中，∠A＝90°，AB＝4，AC＝6，点D为AC中点，点P为AB上的动点，将点P绕点D逆时针旋转90°得到点Q，连接CQ，则线段CQ的最小值为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
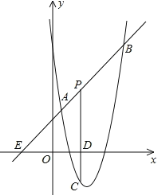
【题目】如图，直线y=x+2与抛物线y=ax2+bx+6（a≠0）相交于A（
，
）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．
（1）求抛物线的解析式；
（2）是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由；
（3）假若△PAC为直角三角形，直接写出点P坐标。
查看答案和解析>>
科目：初中数学 来源： 题型：
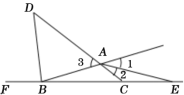
【题目】如图，在△ABC中，∠ABC＜∠BCA＜∠BAC，∠BAC和∠ABC的外角平分线AE、BD分别与BC、CA的延长线交于E、D．若AB＝AE，BD＝BA．则∠BCA的度数为____．
查看答案和解析>>
科目：初中数学 来源： 题型：
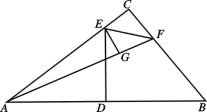
【题目】如图，在△ABC中，∠C＝90°，AB的垂直平分线DE交AC于点E，垂足是D，F是BC上一点，EF平分∠AFC，EG⊥AF于点G．
（1）试判断EC与EG，CF与GF是否相等；（直接写出结果，不要求证明）
（2）求证：AG＝BC；
（3）若AB＝5，AF+BF＝6，求EG的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ACB＝90°．
（1）作出经过点B，圆心O在斜边AB上且与边AC相切于点E的⊙O（要求：用尺规作图，保留作图痕迹，不写作法和证明）
（2）设（1）中所作的⊙O与边AB交于异于点B的另外一点D，若⊙O的直径为5，BC＝4；求DE的长．（如果用尺规作图画不出图形，可画出草图完成（2）问）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】
、
两组卡片共
张，中三张分别写有数字
，
，
，中两张分别写有
，．它们除了数字外没有任何区别．
随机地从中抽取一张，求抽到数字为的概率；
随机地分别从、中各抽取一张，请你用画树状图或列表的方法表示所有等可能的结果，现制定这样一个游戏规则：若选出的两数之积为的倍数，则甲获胜；否则乙获胜．请问这样的游戏规则对甲乙双方公平吗？为什么？
如果不公平请你修改游戏规则使游戏规则对甲乙双方公平．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
