
����Ŀ����֪����ͼ��1������ƽ��ֱ������ϵ�У���A����B�քe��x�ᡢy����������ϣ���C�ڵ�һ���ޣ���ACB��90����AC��BC����A����Ϊ��m��0������C������Ϊn����m2+n2��2m��8n+17��0��
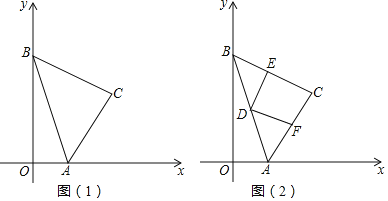
��1���քe�����A����B����C�����ꣻ
��2����ͼ��2������DΪ��AB�е㣬�Ե�DΪ�����ֱ�ǡ�EDF���߷ֱ�BC��E������AC��F������֤��DE��DF������֤��S�ı���DECF��![]() S��ABC��
S��ABC��
��3��������ƽ�����е�G����G�����A�غϣ���ʹ����BCG����BCΪֱ�DZߵĵ���ֱ�������Σ���ֱ��д�����������ĵ�G�����꣮
���𰸡���1����A��1��0������B��0��7������C��4��4������2���ټ��������ڼ���������3����G��-3��3����3��11����7��8��
��������
��1���ɷǸ��Կ���m��n��ֵ���ɡ�AAS����֤��BCM�ա�ACN���ɵ�CM��CN��4��OM��AN��BM��3��������⣻
��2�����ɵ���ֱ�������ε����ʿɵ�BD��CD��AD����ABC����BAC����BCD����ACD��45�㣬AB��CD���ɡ�AAS����֤��BDE�ա�CDF���ɵ�DE��DF��
����ȫ�������ε����ʿɵ�S��BDE��S��CDF�����ɵý��ۣ�
��3��������������ۣ��ɵ���ֱ�������ε����ʺ�ȫ�������ε����ʿ���⣮
��1����ͼ��1��������C��CM��OB��CN��OA��
��m2+n2��2m��8n+17��0��
�ࣨm��1��2+��n��4��2��0��
��m��1��n��4��
���A��1��0����CM��4��
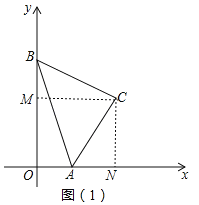
��CM��OB��CN��OA����AOB��90����
���ı���OMCN�Ǿ��Σ�
���MCN��90������ACB��CM��ON��4��CN��OM��
��AN��3����MCN-��MVA����ACB-��MVA
���BCM����ACN��
�� AC��BC����BMC����ANC��
���BCM�ա�ACN��AAS��
��CM��CN��4��OM��AN��BM��3��
���B��0��7������C��4��4����
��2������ͼ��2��������CD��
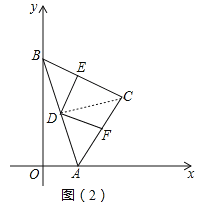
��AC��BC����ACB��90������DΪ��AB�е㣬
��BD��CD��AD����ABC����BAC����BCD����ACD��45����AB��CD
�ߡ�EDF��90������BDC��
���EDF-��EDC����BDC-��EDC
���BDE����CDF��
��BD��CD����ABC����DCA��
���BDE�ա�CDF��AAS��
��DE��DF��
�ڡߡ�BDE�ա�CDF��
��S��BDE��S��CDF��
��S��BDE+S��EDC��S��CDF+S��EDC��
��S��BDC��S�ı���EDFC��
��AD��BD��
��![]()
��S�ı���DECF��![]() S��ABC��
S��ABC��
��3����ͼ��3����
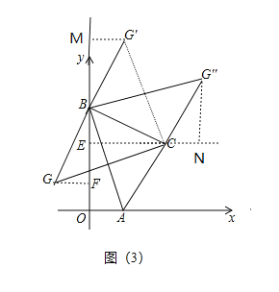
����GBC��90����BG��BCʱ���ҵ�G��BC�·�������G��GF��OB������C��CE��OB��
�ߡ�GBF+��EBC��90������GBF+��BGF��90����
���EBC����BGF��
�ߡ�BEC����BFG��90����BG��BC��
���BGF�ա�CBE��AAS��
��BF��CE��4��GF��BE��
��OF��OB-BF=7-4=3��
���G����3��3����
��![]() ʱ���ҵ�
ʱ���ҵ�![]() ��BC�Ϸ�������
��BC�Ϸ�������![]() ��
��![]() M��OB������C��CE��OB��
M��OB������C��CE��OB��
��![]()
��![]() ��
��
��![]()
��![]()
��BM��CE��4��![]() ��
��
��OM��OB+BM=7+4=11��
��![]() ��
��
��![]() ��
��![]() ʱ����
ʱ����![]() ��BC�Ϸ�������
��BC�Ϸ�������![]() ��
��![]() N��EC������C��CE��OB��
N��EC������C��CE��OB��
��![]()
��![]() ��
��
��![]()
��![]()
��CN��BE��3��![]() ��
��
��EN��4+3=7��
���![]()
������������G����3��3����G(3,11)��G(7,8)


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����̽�������ε��ڽǺ͵�С���У�Сӱ�����¸����ߣ��ӳ���ABC�ı�BC��D����CE��AB������Сӱ�ó��������ڽǺ͵�֤��������
��1����֤����A+��B+��ACB��180�㣻
��2�����CEƽ�֡�ACD��AC��5����BC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
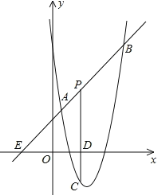
����Ŀ����ͼ��ֱ��y=x+2��������y=ax2+bx+6��a��0���ཻ��A��![]() ��
��![]() ����B��4��m������P���߶�AB������A��B�Ķ��㣬����P��PC��x���ڵ�D�����������ڵ�C��
����B��4��m������P���߶�AB������A��B�Ķ��㣬����P��PC��x���ڵ�D�����������ڵ�C��
��1���������ߵĽ���ʽ��
��2���Ƿ����������P�㣬ʹ�߶�PC�ij������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
��3��������PACΪֱ�������Σ�ֱ��д����P���ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
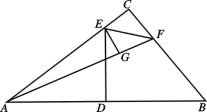
����Ŀ����ͼ������ABC�У���C��90����AB�Ĵ�ֱƽ����DE��AC�ڵ�E��������D��F��BC��һ�㣬EFƽ�֡�AFC��EG��AF�ڵ�G��
��1�����ж�EC��EG��CF��GF�Ƿ���ȣ���ֱ��д���������Ҫ��֤����
��2����֤��AG��BC��
��3����AB��5��AF+BF��6����EG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB��90�㣮
��1������������B��Բ��O��б��AB�������AC�����ڵ�E�ġ�O��Ҫ���ó߹���ͼ��������ͼ�ۼ�����д������֤����
��2���裨1���������ġ�O���AB�������ڵ�B������һ��D������O��ֱ��Ϊ5��BC��4����DE�ij���������ó߹���ͼ������ͼ�Σ��ɻ�����ͼ��ɣ�2���ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ������
������![]() ������
������![]() ���������dz���ɫ�ⶼ��ͬ��С�������������һ������˵����ȷ���ǣ� ��
���������dz���ɫ�ⶼ��ͬ��С�������������һ������˵����ȷ���ǣ� ��
A. һ���Ǻ��� B. �Ǻ�����������Ŀ�������ͬ
C. ��������Ŀ����Ա���������Ŀ����Դ� D. �п����Ǻ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ��
��![]() ���鿨Ƭ��
���鿨Ƭ��![]() �ţ�
�ţ�![]() �����ŷֱ�д������
�����ŷֱ�д������![]() ��
��![]() ��
��![]() ��
��![]() �����ŷֱ�д��
�����ŷֱ�д��![]() ��
��![]() �����dz���������û���κ�����
�����dz���������û���κ�����
![]() ����ش�
����ش�![]() �г�ȡһ�ţ���鵽����Ϊ
�г�ȡһ�ţ���鵽����Ϊ![]() �ĸ��ʣ�
�ĸ��ʣ�
![]() ����طֱ��
����طֱ��![]() ��
��![]() �и���ȡһ�ţ������û���״ͼ���б��ķ�����ʾ���еȿ��ܵĽ�������ƶ�����һ����Ϸ������ѡ��������֮��Ϊ
�и���ȡһ�ţ������û���״ͼ���б��ķ�����ʾ���еȿ��ܵĽ�������ƶ�����һ����Ϸ������ѡ��������֮��Ϊ![]() �ı��������ʤ�������һ�ʤ��������������Ϸ����Լ���˫����ƽ��Ϊʲô��
�ı��������ʤ�������һ�ʤ��������������Ϸ����Լ���˫����ƽ��Ϊʲô��
![]() �������ƽ��������Ϸ����ʹ��Ϸ����Լ���˫����ƽ��
�������ƽ��������Ϸ����ʹ��Ϸ����Լ���˫����ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
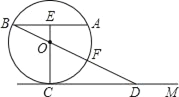
����Ŀ����ͼ����֪��ABΪ��O���ң���ֱ������EΪAB���е㣬EO���ӳ�������O�ཻ��C��CM��AB��BO���ӳ�������O�ཻ��F����CM�ཻ��D��
����֤��EC��CD��
����EO��OC=1��3��CD=4ʱ������O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ϵ�У���ABC���������������ֱ�Ϊ��2��1��������1��3��������3��2��.
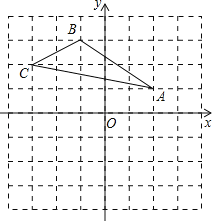
��1����ͼ��������ABC����x��ԳƵġ�A��B��C�䣬��д����A�������Ϊ�� ������B������Ϊ�� ������C�������Ϊ�� ����
��2�����ABC�������
��3������P��a��a��2�����Q����y��Գƣ���PQ��8�����P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com