
【题目】阅读:设试验结果落在某个区域S中每一点的机会均等,用A表示事件“试验结果落在S中的一个小区域M中”,那么事件A发生的概率P(A)![]() .在桌面上放一张50 cm×50 cm的正方形白纸ABCD,⊙O是它的内切圆,小明随机地将1000粒大米撒到该白纸上,其中落在圆内的大米有800粒,由此可得圆周率
.在桌面上放一张50 cm×50 cm的正方形白纸ABCD,⊙O是它的内切圆,小明随机地将1000粒大米撒到该白纸上,其中落在圆内的大米有800粒,由此可得圆周率![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
【题目】小明骑单车上学,当他骑了一段路时起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校以下是他本次上学所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是 米,本次上学途中,小明一共行驶了 米;
(2)小明在书店停留了 分钟,本次上学,小明一共用了 分钟;
(3)在整个上学的途中那个时间段小明骑车速度最快,最快的速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程与时间的函数图象如图所示,下列说法正确的有()个

①快车追上慢车需6小时
②慢车比快车早出发2小时
③快车速度为46km/h
④慢车速度为46km/h
⑤AB两地相距828km
⑥快车14小时到达B地
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是明代数学家程大位的《算法统宗》中的一个问题,其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两(注:明代时1斤= 16两,故有“半斤八两”这个成语.则下列设未知数列方程正确的序号是____.

①设这群人人数为x,根据题意得7x- 4=9x+ 8;
②设这群人人数为x,根据题意得7x+ 4= 9x一8;
③设所分银子的数量为x两,根据题意得![]() =
=![]()
④设所分银子的数量为x两,根据题意得![]() =
=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折线”).

(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;
(2)如图2,双曲线y=![]() 与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,O,E在同一条直线上,∠BOD= 90°,OD是∠COE的角平分线,找出图中与∠DOE互余的角.甲、乙、丙三个同学的答案如下:
甲:只有一个角,是∠AOB:
乙:有两个角,是∠AOB和∠BOC:
丙:有三个角,是∠AOB,∠BOC,∠COD.

(1)请你判断哪个同学的答案是正确的?
(2)请你说明正确答案的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里.
﹣4,﹣|﹣![]() |,0,
|,0,![]() ,﹣3.14,2019,﹣(+5),+1.88,
,﹣3.14,2019,﹣(+5),+1.88,
(1)正数集合:{ _____…};(2)负数集合:{__________…};
(3)分数集合:{_______…};(4)非负整数集合:{_______…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍船只停在C处海域,AB=60(![]() +3)海里,在B处测得C在北偏东45°方向上,A处测得C在北偏西30°方向上,在海岸线AB上有一等他D,测得AD=100海里.
+3)海里,在B处测得C在北偏东45°方向上,A处测得C在北偏西30°方向上,在海岸线AB上有一等他D,测得AD=100海里.
(1)分别求出AC,BC(结果保留根号)
(2)已知在灯塔D周围80海里范围内有暗礁群,在A处海监船沿AC前往C处盘看,图中有无触礁的危险?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与x轴交于A,B两点,与y轴交于点C,顶点为D,点C’是点C关于对称轴的对称点,过点D作DG⊥x轴交x轴于点G,交线段AC于点E。
与x轴交于A,B两点,与y轴交于点C,顶点为D,点C’是点C关于对称轴的对称点,过点D作DG⊥x轴交x轴于点G,交线段AC于点E。
(1)连接DC,求△DCE的周长;
(2)如图2,点P是线段AC上方抛物线上的一点,过P作PH⊥x 轴交x轴于点H,交线段AC于点Q,当四边形PCQC’的面积最大时,在线段PH上有一动点M,在线段DG上有一动点N,在y轴上有一动点E,且满足MN⊥PH,连接AM,MN,NE,DE,求AM+MN+NE+DE的最小值;
(3)如图3,将抛物线沿直线AC进行平移,平移过程中的点D记为D’,点C记为C’,连接D’C’所形成的直线与x轴相交于点G,请问是否存在这样的点G,使得△D’OG为等腰三角形?若存在,求出此时OG的长度,若不存在,请说明理由。


图1 图2
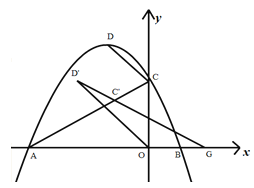
图3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com