Question

【题目】如图1，已知抛物线与x轴交于A,B两点，与y轴交于点C，顶点为D，点C’是点C关于对称轴的对称点，过点D作DG⊥x轴交x轴于点G，交线段AC于点E。

（1）连接DC，求△DCE的周长；

（2）如图2，点P是线段AC上方抛物线上的一点，过P作PH⊥x 轴交x轴于点H，交线段AC于点Q，当四边形PCQC’的面积最大时，在线段PH上有一动点M，在线段DG上有一动点N，在y轴上有一动点E，且满足MN⊥PH，连接AM,MN,NE,DE，求AM+MN+NE+DE的最小值；

（3）如图3，将抛物线沿直线AC进行平移，平移过程中的点D记为D’，点C记为C’，连接D’C’所形成的直线与x轴相交于点G，请问是否存在这样的点G，使得△D’OG为等腰三角形？若存在，求出此时OG的长度，若不存在，请说明理由。

图1 图2

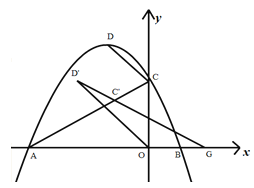
图3

Answer 1

【答案】（1）2（2） （3）OG=或5或或

【解析】分析：(1)根据函数解析式，分别求出点C，D，E的坐标，用勾股定理求CD，CE的长；(2)四边形PCQC′的面积等于PQ与CC′积的一半，CC′是的值不变，即PQ最大时，四边形PCQC′的面积最大，得到P，H的坐标，可求MN的长，分别将AM向MN方向平移MN个单位得到，过轴作的对称点，则＋MN为所求；(3)根据D点的运动路径平行于AC，得直线DD′的解析式为，设D′，用含a的代数式表示点G的坐标，用勾股定理求OG，OD′，GD′的长，分三种情况讨论.

详解：(1)可得，D()对称轴＝－1，

∵直线AC的解析式为，∴，

∴CD＝ ＝；

CE＝ ＝；

DE＝.

∴.

(2)设，

， 的值不变.

当PQ最大时，四边形面积最大，PQ的值最大，且，

当时，PQ最大，此时面积最大， .

， ，

将AM向MN方向平移个单位得到.

过轴作的对称点，连接，交DG于点N，交y轴于点E，过N作MN∥于轴交PH于点M，

此时最小，最小值＝.

(3)D点的运动路径平行于AC， ，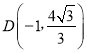

∴，设.

∵∠DCA＝60°，DC∥.

∴∠CG＝60°，∠AG＝120°.

∵∠CAO＝30°，∴∠＝30°.

∴直线D′E的解析式为y＝－，∴.

由勾股定理得：

，

，

.

①时， ，∴OG＝0(舍)；

②时， ，∴OG＝；

③时， ，∴OG＝.

综上所述：OG＝或.