
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.

(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
【答案】(1)证明见解析(2)40°
【解析】(1)证明:∵四边形ABCD是菱形,∴AB=CD,AB∥CD。
又∵BE=AB,∴BE=CD,BE∥CD。∴四边形BECD是平行四边形。
∴BD=EC。
(2)解:∵四边形BECD是平行四边形,∴BD∥CE,∴∠ABO=∠E=50°。
又∵四边形ABCD是菱形,∴AC丄BD。∴∠BAO=90°﹣∠ABO=40°
(1)根据菱形的对边平行且相等可得AB=CD,AB∥CD,然后证明得到BE=CD,BE∥CD,从而证明四边形BECD是平行四边形,再根据平行四边形的对边相等即可得证。
(2)根据两直线平行,同位角相等求出∠ABO的度数,再根据菱形的对角线互相垂直可得AC⊥BD,然后根据直角三角形两锐角互余计算即可得解。


科目:初中数学 来源: 题型:
【题目】一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程与时间的函数图象如图所示,下列说法正确的有()个

①快车追上慢车需6小时
②慢车比快车早出发2小时
③快车速度为46km/h
④慢车速度为46km/h
⑤AB两地相距828km
⑥快车14小时到达B地
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里.
﹣4,﹣|﹣![]() |,0,
|,0,![]() ,﹣3.14,2019,﹣(+5),+1.88,
,﹣3.14,2019,﹣(+5),+1.88,
(1)正数集合:{ _____…};(2)负数集合:{__________…};
(3)分数集合:{_______…};(4)非负整数集合:{_______…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍船只停在C处海域,AB=60(![]() +3)海里,在B处测得C在北偏东45°方向上,A处测得C在北偏西30°方向上,在海岸线AB上有一等他D,测得AD=100海里.
+3)海里,在B处测得C在北偏东45°方向上,A处测得C在北偏西30°方向上,在海岸线AB上有一等他D,测得AD=100海里.
(1)分别求出AC,BC(结果保留根号)
(2)已知在灯塔D周围80海里范围内有暗礁群,在A处海监船沿AC前往C处盘看,图中有无触礁的危险?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果过抛物线![]() 与y的交点作y轴的垂线与该抛物线有另一个交点,并且这两点与该抛物线的顶点构成正三角形,那么我们称这个抛物线为正三角抛物线.
与y的交点作y轴的垂线与该抛物线有另一个交点,并且这两点与该抛物线的顶点构成正三角形,那么我们称这个抛物线为正三角抛物线.
(1)抛物线![]() 正三角抛物线;(填“是”或“不是”)
正三角抛物线;(填“是”或“不是”)
(2)如图,已知二次函数![]() (m > 0)的图像是正三角抛物线,它与x轴交于A、B两点(点A在点B的左侧),点E在y轴上,当∠AEB=2∠ABE时,求出点E的坐标.
(m > 0)的图像是正三角抛物线,它与x轴交于A、B两点(点A在点B的左侧),点E在y轴上,当∠AEB=2∠ABE时,求出点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)用含有![]() 的式子表示判别式
的式子表示判别式![]() ________;
________;
(2)当![]() 在什么范围内取值时,方程有两个不相等的实数根;
在什么范围内取值时,方程有两个不相等的实数根;
(3)若该方程有两个不相等的实数根![]() ,
,![]() ,问当
,问当![]() 取何值时
取何值时![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对七年级全体学生进行了期中测试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了下面的条形图和扇形图(图1和图2均不完整)请根据图中所给的信息,解答下列问题:
(1)求抽取学生的人数,请将表示成绩类别为“中”的条形图补充完整;
(2)求扇形图中表示成绩类别为“优“的扇形所占的百分数;
(3)如果该校七年级共有300人参加期中测试,请估计成绩在“良”及“良”以上的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与x轴交于A,B两点,与y轴交于点C,顶点为D,点C’是点C关于对称轴的对称点,过点D作DG⊥x轴交x轴于点G,交线段AC于点E。
与x轴交于A,B两点,与y轴交于点C,顶点为D,点C’是点C关于对称轴的对称点,过点D作DG⊥x轴交x轴于点G,交线段AC于点E。
(1)连接DC,求△DCE的周长;
(2)如图2,点P是线段AC上方抛物线上的一点,过P作PH⊥x 轴交x轴于点H,交线段AC于点Q,当四边形PCQC’的面积最大时,在线段PH上有一动点M,在线段DG上有一动点N,在y轴上有一动点E,且满足MN⊥PH,连接AM,MN,NE,DE,求AM+MN+NE+DE的最小值;
(3)如图3,将抛物线沿直线AC进行平移,平移过程中的点D记为D’,点C记为C’,连接D’C’所形成的直线与x轴相交于点G,请问是否存在这样的点G,使得△D’OG为等腰三角形?若存在,求出此时OG的长度,若不存在,请说明理由。


图1 图2
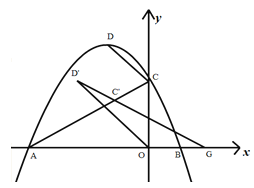
图3
查看答案和解析>>
科目:初中数学 来源: 题型:
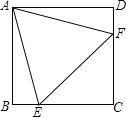
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=![]() .
.
其中正确的序号是 (把你认为正确的都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com