
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)用含有![]() 的式子表示判别式
的式子表示判别式![]() ________;
________;
(2)当![]() 在什么范围内取值时,方程有两个不相等的实数根;
在什么范围内取值时,方程有两个不相等的实数根;
(3)若该方程有两个不相等的实数根![]() ,
,![]() ,问当
,问当![]() 取何值时
取何值时![]() .
.
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,晚上小亮在广场上乘凉,图中线段AB表示站在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯.
请你再图中画出小亮在照明灯P照射下的影子BC;
如果灯杆高PO=12m,小亮的身高AB=1.6m,小亮与灯杆的距离BO=13m,请求出小亮影子的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
数学活动课上,小红画了如图1所示的两个共用直角顶点的等腰直角三角形![]() 与等腰直角三角形
与等腰直角三角形![]() ,其中
,其中![]() ,
,![]() ,连接
,连接![]() ,
,![]() 、
、![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 、
、![]() 的中点,连接
的中点,连接![]() 、
、![]() .
.
操作发现:
小红发现了:![]() 、
、![]() 有一定的关系,数量关系为_____________________________;位置关系为_________________.
有一定的关系,数量关系为_____________________________;位置关系为_________________.

类比思考:
如图2,在图1的基础上,将等腰直角三角形![]() 绕点
绕点![]() 旋转一定的角度,其它条件都不变,小红发现的结论还成立吗?请说明理由.(提示:连接
旋转一定的角度,其它条件都不变,小红发现的结论还成立吗?请说明理由.(提示:连接![]() 、
、![]() 并延长交于一点
并延长交于一点![]() )
)
深入探究:
在上述类比思考的基础上,小红做了进一步的探究.如图3,作任意一个三角形![]() ,其中
,其中![]() ,在三角形外侧以
,在三角形外侧以![]() 为腰作等腰直角三角形
为腰作等腰直角三角形![]() ,以
,以![]() 为腰作等腰直角三角形
为腰作等腰直角三角形![]() ,分别取斜边
,分别取斜边![]() 、
、![]() 与边
与边![]() 的中点
的中点![]() 、
、![]() 、
、![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,试判断三角形
,试判断三角形![]() 的形状,并说明理由.
的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A,B,O,C为数轴上四点,点A对应数![]() ,点O对应0,点C对应3,
,点O对应0,点C对应3,![]() (AB表示点A到点B的距离).
(AB表示点A到点B的距离).

(1)填空:点C到原点O的距离______,点B对应的数______.(用含有a的式子)
(2)如图2,将一刻度尺放在数轴上,刻度尺上“6cm”和“8.7cm”分别对应数轴上的点O和点C,若![]() ,求a的值和点A在刻度尺上对应的刻度。
,求a的值和点A在刻度尺上对应的刻度。
(3)如图3,在(2)的条件下,点A以1单位长度/秒的速度向右运动,同时点C向左运动,若运动3秒时,点A和点C到原点O的距离相等,求点C的运动速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.

(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
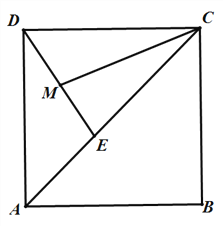
【题目】在菱形ABCD中,AC是对角线,CD=CE,连接DE,点M是线段DE的中点.
(1)如图1,连接CM,若AC=16,CD=10,求DE的长
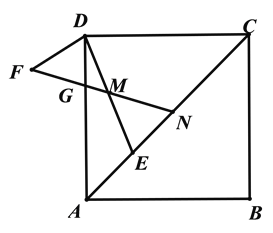
(2)如图2,点F在菱形的外部,DF=DM,且∠CDA=∠FDE,连接FM交AD于点G,FM的延长线交AC于点N,求证:CN=AG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提升城市容貌,规范城市管理.我区城管某巡逻车在一条东西方向的公路上巡逻,规定向东为正,向西为负.某天,汽车从出发点开始所走的路程分别为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:千米).队长要求汇报位置.
(单位:千米).队长要求汇报位置.
(1)此时,驾驶员如何向队长描述他的位置?
(2)如果队长命令他马上返回到出发点,这次巡逻(从出发点开始到最后又返回出发点)共耗油多少升?(已知每千米耗油![]() 升)
升)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平行四边形ABCD,DE⊥AB.垂足E在BA的延长线上,BF⊥DC,垂足F在DC的延长线上.

(1)求证:四边形BEDF是矩形;
(2)如图2,若M、N分别为AD、BC的中点,连接EM、EN、FM、FN,求证:四边形EMFN是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4 cm,则球的半径长是( )

A. 2cm B. 2.5cm C. 3cm D. 4cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com