
【题目】如图1,平行四边形ABCD,DE⊥AB.垂足E在BA的延长线上,BF⊥DC,垂足F在DC的延长线上.

(1)求证:四边形BEDF是矩形;
(2)如图2,若M、N分别为AD、BC的中点,连接EM、EN、FM、FN,求证:四边形EMFN是平行四边形.
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:(1)根据平行四边形的性质和矩形的判定证明即可;
(2)利用平行四边形的性质和矩形的性质得出BN=DM,BF=DE,∠NBF=∠MDE,进而证明△BNF≌△DME,得出EM=FN,同理得出EN=MF,进而证明四边形EMFN是平行四边形.
试题解析:
(1)∵平行四边形ABCD,
∴AB∥CD,
∴∠ABF+∠F=180°,∠FDE+∠E=180°,
∵DE⊥AB.BF⊥DC,
∴∠E=90°,∠F=90°,
∴∠ABF=90°,∠FDE=90°,
∴四边形BEDF是矩形;
(2)∵平行四边形ABCD,四边形BEDF是矩形,
∴∠NBF+∠BCF=90°,∠EDM+∠ADC=90°,AD∥BC,AD=BC,BF=DE,
∴∠ADC=∠BCF,
∴∠NBF=∠MDE,
∵M、N分别为AD、BC的中点,
∴BN=DM,
在△BNF与△DME中

∴△BNF≌△DME(SAS),
∴EM=FN,
同理可得:EN=MF,
∴四边形EMFN是平行四边形.


科目:初中数学 来源: 题型:
【题目】如图,点A,O,E在同一条直线上,∠BOD= 90°,OD是∠COE的角平分线,找出图中与∠DOE互余的角.甲、乙、丙三个同学的答案如下:
甲:只有一个角,是∠AOB:
乙:有两个角,是∠AOB和∠BOC:
丙:有三个角,是∠AOB,∠BOC,∠COD.

(1)请你判断哪个同学的答案是正确的?
(2)请你说明正确答案的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)用含有![]() 的式子表示判别式
的式子表示判别式![]() ________;
________;
(2)当![]() 在什么范围内取值时,方程有两个不相等的实数根;
在什么范围内取值时,方程有两个不相等的实数根;
(3)若该方程有两个不相等的实数根![]() ,
,![]() ,问当
,问当![]() 取何值时
取何值时![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,设先发出车辆行驶的时间为 xh , 两车之间的距离为ykm,图中的折线表示 y与x之间的函数关系。根据图象回答下列问题:
(1)慢车的速度为________ km/h,快车的速度为__________km/h;
(2)求线段CD所表示的y与x之间的函数关系式,并写出自变量 x的取值范围;
(3)当 x取何值时,两车之间的距离为300 km?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与x轴交于A,B两点,与y轴交于点C,顶点为D,点C’是点C关于对称轴的对称点,过点D作DG⊥x轴交x轴于点G,交线段AC于点E。
与x轴交于A,B两点,与y轴交于点C,顶点为D,点C’是点C关于对称轴的对称点,过点D作DG⊥x轴交x轴于点G,交线段AC于点E。
(1)连接DC,求△DCE的周长;
(2)如图2,点P是线段AC上方抛物线上的一点,过P作PH⊥x 轴交x轴于点H,交线段AC于点Q,当四边形PCQC’的面积最大时,在线段PH上有一动点M,在线段DG上有一动点N,在y轴上有一动点E,且满足MN⊥PH,连接AM,MN,NE,DE,求AM+MN+NE+DE的最小值;
(3)如图3,将抛物线沿直线AC进行平移,平移过程中的点D记为D’,点C记为C’,连接D’C’所形成的直线与x轴相交于点G,请问是否存在这样的点G,使得△D’OG为等腰三角形?若存在,求出此时OG的长度,若不存在,请说明理由。


图1 图2
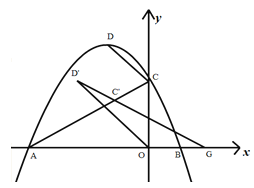
图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是关于
是关于![]() 的二次多项式,且二次项系数和一次项系数分别为
的二次多项式,且二次项系数和一次项系数分别为![]() 和
和![]() ,在数轴上
,在数轴上![]() 、
、![]() 、
、![]() 三点所对应的数分别是
三点所对应的数分别是![]() 、
、![]() 、
、![]() .
.
![]()
(1)有一动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度向左运动,多少秒后,
个单位的速度向左运动,多少秒后,![]() 到
到![]() 、
、![]() 、
、![]() 的距离和为
的距离和为![]() 个单位?
个单位?
(2)在(1)的条件下,当点![]() 移动到点
移动到点![]() 时立即掉头,速度不变,同时点
时立即掉头,速度不变,同时点![]() 和点
和点![]() 分别从点
分别从点![]() 和点
和点![]() 出发,向右运动,点
出发,向右运动,点![]() 的速度
的速度![]() 个单位
个单位![]() 秒,点
秒,点![]() 的速度
的速度![]() 个单位
个单位![]() 秒.设点
秒.设点![]() 、
、![]() 、
、![]() 所对应的数分别是
所对应的数分别是![]() 、
、![]() 、
、![]() ,点
,点![]() 出发的时间为
出发的时间为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个四位自然数n,如果n满足各个数位上的数字互不相同且均不为0,它的千位数字与个位数字之和等于百位数字与十位数字之和,那么称这个数n为“平衡数”.对于一个“平衡数”,从千位数字开始顺次取出三个数字构成四个三位数,把这四个三位数的和与222的商记为F(n). 例如:n=1526,因为1+6=2+5,所以1526是一个“平衡数”,从千位数字开始顺次取出三个数字构成的四个三位数分别为152、526、261、615,这四个三位数的和为:152+526+261+615=1554,1154![]() 222=7,所以F(1526)=7.
222=7,所以F(1526)=7.
![]() 写出最小和最大的“平衡数”n,并求出对应的F(n)的值;
写出最小和最大的“平衡数”n,并求出对应的F(n)的值;
![]() 若s,t都是“平衡数”,其中s=10x+y+3201,t=1000m+10n+126(
若s,t都是“平衡数”,其中s=10x+y+3201,t=1000m+10n+126(![]() ,
, ![]() ,
, ![]() ,
, ![]() ,x, y, m, n都是整数),规定:
,x, y, m, n都是整数),规定: ![]() ,当F(s)+F(t)是一个完全平方数时,求k的最大值.
,当F(s)+F(t)是一个完全平方数时,求k的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com