
°æƒø°ø“—÷™![]() «πÿ”⁄
«πÿ”⁄![]() µƒ∂˛¥Œ∂‡œÓ Ω£¨«“∂˛¥ŒœÓœµ ˝∫Õ“ª¥ŒœÓœµ ˝∑÷±Œ™
µƒ∂˛¥Œ∂‡œÓ Ω£¨«“∂˛¥ŒœÓœµ ˝∫Õ“ª¥ŒœÓœµ ˝∑÷±Œ™![]() ∫Õ
∫Õ![]() £¨‘⁄ ˝÷·…œ
£¨‘⁄ ˝÷·…œ![]() °¢
°¢![]() °¢
°¢![]() »˝µ„À˘∂‘”¶µƒ ˝∑÷± «
»˝µ„À˘∂‘”¶µƒ ˝∑÷± «![]() °¢
°¢![]() °¢
°¢![]() .
.
![]()
£®1£©”–“ª∂ص„![]() ¥”µ„
¥”µ„![]() ≥ˆ∑¢£¨“‘√ø√Î
≥ˆ∑¢£¨“‘√ø√Î![]() ∏ˆµ•ŒªµƒÀŸ∂»œÚ◊Û‘À∂Ø£¨∂‡…Ÿ√Î∫Û£¨
∏ˆµ•ŒªµƒÀŸ∂»œÚ◊Û‘À∂Ø£¨∂‡…Ÿ√Î∫Û£¨![]() µΩ
µΩ![]() °¢
°¢![]() °¢
°¢![]() µƒæ‡¿Î∫ÕŒ™
µƒæ‡¿Î∫ÕŒ™![]() ∏ˆµ•Œª£ø
∏ˆµ•Œª£ø
£®2£©‘⁄£®1£©µƒÃıº˛œ¬£¨µ±µ„![]() “∆∂ØµΩµ„
“∆∂ØµΩµ„![]() ±¡¢º¥µÙÕ∑£¨ÀŸ∂»≤ª±‰£¨Õ¨ ±µ„
±¡¢º¥µÙÕ∑£¨ÀŸ∂»≤ª±‰£¨Õ¨ ±µ„![]() ∫Õµ„
∫Õµ„![]() ∑÷±¥”µ„
∑÷±¥”µ„![]() ∫Õµ„
∫Õµ„![]() ≥ˆ∑¢£¨œÚ”“‘À∂Ø£¨µ„
≥ˆ∑¢£¨œÚ”“‘À∂Ø£¨µ„![]() µƒÀŸ∂»
µƒÀŸ∂»![]() ∏ˆµ•Œª
∏ˆµ•Œª![]() √Σ¨µ„
√Σ¨µ„![]() µƒÀŸ∂»
µƒÀŸ∂»![]() ∏ˆµ•Œª
∏ˆµ•Œª![]() √Î.…˵„
√Î.…˵„![]() °¢
°¢![]() °¢
°¢![]() À˘∂‘”¶µƒ ˝∑÷± «
À˘∂‘”¶µƒ ˝∑÷± «![]() °¢
°¢![]() °¢
°¢![]() £¨µ„
£¨µ„![]() ≥ˆ∑¢µƒ ±º‰Œ™
≥ˆ∑¢µƒ ±º‰Œ™![]() £¨µ±
£¨µ±![]() ±£¨«Û
±£¨«Û![]() µƒ÷µ.
µƒ÷µ.
°æ¥∞∏°ø£®1£©2√Σª£®2£©8t-26
°æΩ‚Œˆ°ø
£®1£©œ»∏˘æ›Ã‚“‚«Û≥ˆa°¢b°¢cµƒ÷µ£¨‘Ÿ∏˘æ›Õº–Œµ√µΩ£∫![]() µΩ
µΩ![]() °¢
°¢![]() °¢
°¢![]() µƒæ‡¿Î∫ÕŒ™
µƒæ‡¿Î∫ÕŒ™![]() ∏ˆµ•Œª£¨‘Ú¥À ±P“ª∂®‘⁄B∫Õ‘≠µ„÷ƺ‰£¨…˵„P±Ì 浃 ˝Œ™x£¨¡–≥ˆ∑Ω≥ã¨Ω‚∑Ω≥㨥”∂¯«Ûµ√ ±º‰£ª
∏ˆµ•Œª£¨‘Ú¥À ±P“ª∂®‘⁄B∫Õ‘≠µ„÷ƺ‰£¨…˵„P±Ì 浃 ˝Œ™x£¨¡–≥ˆ∑Ω≥ã¨Ω‚∑Ω≥㨥”∂¯«Ûµ√ ±º‰£ª
£®2£©œ»«Û≥ˆµ„P◊∑…œµ„Mµƒ ±º‰Œ™![]() √Σ¨µ„N◊∑…œµ„Mµƒ ±º‰Œ™
√Σ¨µ„N◊∑…œµ„Mµƒ ±º‰Œ™![]() £¨µ„N◊∑…œµ„Pµƒ ±º‰Œ™
£¨µ„N◊∑…œµ„Pµƒ ±º‰Œ™![]() £¨”…¥Àª≠≥ˆ∂‘”¶µƒÕº–Œ£¨‘Ÿ¿˚”√æ¯∂‘÷µµƒ–‘÷ «ÛΩ‚.
£¨”…¥Àª≠≥ˆ∂‘”¶µƒÕº–Œ£¨‘Ÿ¿˚”√æ¯∂‘÷µµƒ–‘÷ «ÛΩ‚.
£®1£©“ÚŒ™![]() «πÿ”⁄
«πÿ”⁄![]() µƒ∂˛¥Œ∂‡œÓ Ω£¨«“∂˛¥ŒœÓœµ ˝∫Õ“ª¥ŒœÓœµ ˝∑÷±Œ™
µƒ∂˛¥Œ∂‡œÓ Ω£¨«“∂˛¥ŒœÓœµ ˝∫Õ“ª¥ŒœÓœµ ˝∑÷±Œ™![]() ∫Õ
∫Õ![]() £¨
£¨
À˘“‘a=10,b=6,c=-3,
µ±µ„P‘⁄A°¢B¡Ωµ„÷ƺ‰ ±£¨≤ªø…ƒ‹¥Ê‘⁄µ„![]() µΩ
µΩ![]() °¢
°¢![]() °¢
°¢![]() µƒæ‡¿Î∫ÕŒ™
µƒæ‡¿Î∫ÕŒ™![]() ∏ˆµ•Œª£ª
∏ˆµ•Œª£ª
µ±µ„P‘⁄µ„C∫Õ‘≠µ„÷ƺ‰ ±£¨≤ªø…ƒ‹¥Ê‘⁄µ„![]() µΩ
µΩ![]() °¢
°¢![]() °¢
°¢![]() µƒæ‡¿Î∫ÕŒ™
µƒæ‡¿Î∫ÕŒ™![]() ∏ˆµ•Œª£ª
∏ˆµ•Œª£ª
µ±µ„P‘⁄µ„B∫Õ‘≠µ„÷ƺ‰ ±£¨…ËPµ„±Ì 浃 ˝Œ™x£¨‘Ú£∫
x+3+(6-x)+(10-x)=15
Ω‚µ√x=4,
À˘“‘AP=10-4=6,
À˘“‘µ„P‘À∂صƒ ±º‰Œ™![]() √Σª
√Σª
£®2£©“ÚŒ™µ„P◊∑…œµ„Mµƒ ±º‰Œ™![]() √Σ¨µ„N◊∑…œµ„Mµƒ ±º‰Œ™
√Σ¨µ„N◊∑…œµ„Mµƒ ±º‰Œ™![]() £¨µ„N◊∑…œµ„Pµƒ ±º‰Œ™
£¨µ„N◊∑…œµ„Pµƒ ±º‰Œ™![]() £¨«“
£¨«“![]() £¨
£¨
À˘“‘¥À ±µ„∂‘”¶µƒM°¢N°¢PµƒŒª÷√»ÁÕºÀ˘ æ,∂‘”¶µƒ ˝Œ™![]() =3t+6°¢
=3t+6°¢![]() =t+10°¢
=t+10°¢![]() =5t-3
=5t-3
![]()
°‡![]()
=3t+6-(t+10)+(5t-3)-(t+10)-[(3t+6)-(5t-3)]
=3t+6-t-10+5t-3-t-10-3t-6+5t-3
=8t-26.



| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø◊€∫œ”Î µº˘
˝—ߪÓ∂ØøŒ…œ£¨–°∫Ϫ≠¡À»ÁÕº1À˘ 浃¡Ω∏ˆπ≤”√÷±Ω«∂•µ„µƒµ»—¸÷±Ω«»˝Ω«–Œ![]() ”ε»—¸÷±Ω«»˝Ω«–Œ
”ε»—¸÷±Ω«»˝Ω«–Œ![]() £¨∆‰÷–
£¨∆‰÷–![]() £¨
£¨![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨
£¨![]() °¢
°¢![]() °¢
°¢![]() ∑÷±Œ™±fl
∑÷±Œ™±fl![]() °¢
°¢![]() °¢
°¢![]() µƒ÷–µ„£¨¡¨Ω”
µƒ÷–µ„£¨¡¨Ω”![]() °¢
°¢![]() .
.
≤Ÿ◊˜∑¢œ÷£∫
–°∫Ï∑¢œ÷¡À£∫![]() °¢
°¢![]() ”–“ª∂®µƒπÿœµ£¨ ˝¡øπÿœµŒ™_____________________________£ªŒª÷√πÿœµŒ™_________________.
”–“ª∂®µƒπÿœµ£¨ ˝¡øπÿœµŒ™_____________________________£ªŒª÷√πÿœµŒ™_________________.

¿‡±»Àºøº£∫
»ÁÕº2£¨‘⁄Õº1µƒª˘¥°…œ£¨Ω´µ»—¸÷±Ω«»˝Ω«–Œ![]() »∆µ„
»∆µ„![]() –˝◊™“ª∂®µƒΩ«∂»£¨∆‰À¸Ãıº˛∂º≤ª±‰£¨–°∫Ï∑¢œ÷µƒΩ·¬€ªπ≥…¡¢¬£ø«ÎÀµ√˜¿Ì”….£®Ã· æ£∫¡¨Ω”
–˝◊™“ª∂®µƒΩ«∂»£¨∆‰À¸Ãıº˛∂º≤ª±‰£¨–°∫Ï∑¢œ÷µƒΩ·¬€ªπ≥…¡¢¬£ø«ÎÀµ√˜¿Ì”….£®Ã· æ£∫¡¨Ω”![]() °¢
°¢![]() ≤¢—”≥§Ωª”⁄“ªµ„
≤¢—”≥§Ωª”⁄“ªµ„![]() £©
£©
…Ó»ÎÃΩæø£∫
‘⁄…œ ˆ¿‡±»Àºøºµƒª˘¥°…œ£¨–°∫Ï◊ˆ¡ÀΩ¯“ª≤ΩµƒÃΩæø.»ÁÕº3£¨◊˜»Œ“‚“ª∏ˆ»˝Ω«–Œ![]() £¨∆‰÷–
£¨∆‰÷–![]() £¨‘⁄»˝Ω«–ŒÕ‚≤‡“‘
£¨‘⁄»˝Ω«–ŒÕ‚≤‡“‘![]() Œ™—¸◊˜µ»—¸÷±Ω«»˝Ω«–Œ
Œ™—¸◊˜µ»—¸÷±Ω«»˝Ω«–Œ![]() £¨“‘
£¨“‘![]() Œ™—¸◊˜µ»—¸÷±Ω«»˝Ω«–Œ
Œ™—¸◊˜µ»—¸÷±Ω«»˝Ω«–Œ![]() £¨∑÷±»°–±±fl
£¨∑÷±»°–±±fl![]() °¢
°¢![]() ”αfl
”αfl![]() µƒ÷–µ„
µƒ÷–µ„![]() °¢
°¢![]() °¢
°¢![]() £¨¡¨Ω”
£¨¡¨Ω”![]() °¢
°¢![]() °¢
°¢![]() £¨ ‘≈–∂œ»˝Ω«–Œ
£¨ ‘≈–∂œ»˝Ω«–Œ![]() µƒ–Œ◊¥£¨≤¢Àµ√˜¿Ì”….
µƒ–Œ◊¥£¨≤¢Àµ√˜¿Ì”….

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡À÷…˝≥« –»›√≤£¨πÊ∑∂≥« –π‹¿Ì.Œ“«¯≥«π‹ƒ≥—≤¬fl≥µ‘⁄“ªÃı∂´Œ˜∑ΩœÚµƒπ´¬∑…œ—≤¬fl£¨πÊ∂®œÚ∂´Œ™’˝£¨œÚŒ˜Œ™∏∫.ƒ≥ÃÏ£¨∆˚≥µ¥”≥ˆ∑¢µ„ø™ ºÀ˘◊flµƒ¬∑≥Ã∑÷±Œ™£∫![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £®µ•Œª£∫«ß√◊£©.∂”≥§“™«Ûª„±®Œª÷√.
£®µ•Œª£∫«ß√◊£©.∂”≥§“™«Ûª„±®Œª÷√.
£®1£©¥À ±£¨º› ª‘±»Á∫ŒœÚ∂”≥§√Ë ˆÀ˚µƒŒª÷√£ø
£®2£©»Áπ˚∂”≥§√¸¡ÓÀ˚¬Ì…œ∑µªÿµΩ≥ˆ∑¢µ„£¨’‚¥Œ—≤¬fl£®¥”≥ˆ∑¢µ„ø™ ºµΩ◊Ó∫Û”÷∑µªÿ≥ˆ∑¢µ„£©π≤∫ƒ”Õ∂‡…Ÿ…˝£ø£®“—÷™√ø«ß√◊∫ƒ”Õ![]() …˝£©
…˝£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£¨∆Ω––Àƒ±fl–ŒABCD£¨DE°ÕAB£Æ¥π◊„E‘⁄BAµƒ—”≥§œfl…œ£¨BF°ÕDC£¨¥π◊„F‘⁄DCµƒ—”≥§œfl…œ£Æ

£®1£©«Û÷§£∫Àƒ±fl–ŒBEDF «æÿ–Œ£ª
£®2£©»ÁÕº2£¨»ÙM°¢N∑÷±Œ™AD°¢BCµƒ÷–µ„£¨¡¨Ω”EM°¢EN°¢FM°¢FN£¨«Û÷§£∫Àƒ±fl–ŒEMFN «∆Ω––Àƒ±fl–Œ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø ˝—ß–À»§–°◊È—–æøƒ≥–Õ∫≈¿‰πÒŒ¬∂»µƒ±‰ªØ«Èøˆ£¨∑¢œ÷∏√¿‰πÒµƒπ§◊˜π˝≥à «£∫
µ±Œ¬∂»¥ÔµΩ…Ë∂®Œ¬∂»©Å20°Ê ±£¨÷∆¿‰Õ£÷𣨥À∫Û¿‰πÒ÷–µƒŒ¬∂»ø™ º÷Ω•…œ…˝£¨µ±…œ…˝µΩ©Å4°Ê ±£¨÷∆¿‰ø™ º£¨Œ¬∂»ø™ º÷Ω•œ¬Ωµ£¨µ±¿‰πÒ◊‘∂Ø÷∆¿‰÷¡“ª20°Ê ±£¨÷∆¿‰‘Ÿ¥ŒÕ£÷π£¨£Æ£Æ
∞¥’’“‘…œ∑Ω Ω—≠ª∑Ω¯––
Õ¨—ß√«º«¬º¡À44min ƒ⁄15∏ˆ ±º‰µ„¿‰πÒ÷–µƒŒ¬∂»y£®°Ê£© ÀÊ ±º‰x£®min£© µƒ±‰ªØ«Èøˆ£¨÷∆≥…œ¬±Ì£∫
±º‰x/min | °≠ | 4 | 8 | 10 | 16 | 20 | 21 | 22 | 23 | 24 | 28 | 30 | 36 | 40 | 42 | 44 | °≠ |
Œ¬∂»y/°Ê | °≠ | ©Å20 | ©Å10 | ©Å8°° | ©Å5 | ©Å4 | ©Å8 | ©Å12 | ©Å16 | ©Å20 | ©Å10°° | ©Å8 | ©Å5 | ©Å4 | °°a | ©Å20 | °≠ |
£®1£©Õ®π˝∑÷Œˆ∑¢œ÷£¨¿‰πÒ÷–µƒŒ¬∂»y « ±º‰xµƒ∫Ø ˝£Æ
¢Ÿµ±4°‹x£º20 ±£¨–¥≥ˆ“ª∏ˆ∑˚∫œ±Ì÷– ˝æ›µƒ∫Ø ˝Ω‚Œˆ Ω°° °°£ª
¢⁄µ±20°‹x£º24 ±£¨–¥≥ˆ“ª∏ˆ∑˚∫œ±Ì÷– ˝æ›µƒ∫Ø ˝Ω‚Œˆ Ω°° °°£ª
£®2£©Œ¬∂»≤ªµÕ”⁄©Å8°Êµƒ≥÷–¯ ±º‰Œ™°° °°min£ª
£®3£©Aµƒ÷µŒ™°° °°£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
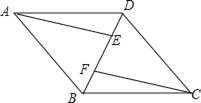
°æƒø°ø“—÷™£∫»ÁÕº£¨Àƒ±fl–ŒABCD «∆Ω––Àƒ±fl–Œ£¨AE°ŒCF£¨«“∑÷±Ωª∂‘Ω«œflBD”⁄µ„E£¨F£Æ
£®1£©«Û÷§£∫°˜AEB°’°˜CFD£ª
£®2£©¡¨Ω”AF£¨CE£¨»Ù°œAFE=°œCFE£¨«Û÷§£∫Àƒ±fl–ŒAFCE «¡‚–Œ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™µ„P «![]() ∂‘Ω«œflBD…œµƒ“ªµ„£¨∑÷±π˝µ„B°¢D◊˜APµƒ¥πœfl£¨¥π◊„∑÷±Œ™µ„E°¢F£¨
∂‘Ω«œflBD…œµƒ“ªµ„£¨∑÷±π˝µ„B°¢D◊˜APµƒ¥πœfl£¨¥π◊„∑÷±Œ™µ„E°¢F£¨
£®1£©»ÁÕº1£¨»Ùµ„PŒ™BD÷–µ„£¨°œBAP=30°„£¨AD=5£¨CD=8£¨«ÛAFµƒ≥§£ª
£®2£©»ÁÕº2£¨»Ùµ„E‘⁄CD…œ£¨BE=DE£¨—”≥§DF÷¡G£¨ πDG=AB£¨µ„H‘⁄BD…œ£¨¡¨Ω”AH°¢GH°¢EH°¢FH£¨»Ù°œG=°œBAH£¨«Û÷§£∫HE=HF£Æ


≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∞—«Ú∑≈‘⁄≥§∑ΩÃÂ÷Ω∫–ƒ⁄£¨«Úµƒ“ª≤ø∑÷¬∂≥ˆ∫–Õ‚£¨∆‰Ωÿ√Ê»ÁÕºÀ˘ 棨“—÷™EF=CD=4 cm£¨‘Ú«Úµƒ∞Îæ∂≥§ «£®°°°°£©

A. 2cm B. 2.5cm C. 3cm D. 4cm
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∞—œ¬¡–“ª‘™∂˛¥Œ∑Ω≥êØ≥…“ª∞„ Ω£¨≤¢–¥≥ˆ∑Ω≥Ã÷–µƒ∏˜œÓº∞∏˜œÓµƒœµ ˝£Æ
£®1£©![]() ;
;
“ª∞„ Ω£∫_________________£Æ
∂˛¥ŒœÓŒ™____£¨∂˛¥ŒœÓœµ ˝Œ™____£¨“ª¥ŒœÓŒ™____£¨
“ª¥ŒœÓœµ ˝Œ™____£¨≥£ ˝œÓŒ™____£Æ
£®2£©![]() £ª
£ª
“ª∞„ Ω£∫_________________£Æ
∂˛¥ŒœÓŒ™____£¨∂˛¥ŒœÓœµ ˝Œ™____£¨“ª¥ŒœÓŒ™____£¨
“ª¥ŒœÓœµ ˝Œ™____£¨≥£ ˝œÓŒ™____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com