
【题目】数学兴趣小组研究某型号冷柜温度的变化情况,发现该冷柜的工作过程是:
当温度达到设定温度﹣20℃时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到﹣4℃时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至一20℃时,制冷再次停止,..
按照以上方式循环进行
同学们记录了44min 内15个时间点冷柜中的温度y(℃) 随时间x(min) 的变化情况,制成下表:
时间x/min | … | 4 | 8 | 10 | 16 | 20 | 21 | 22 | 23 | 24 | 28 | 30 | 36 | 40 | 42 | 44 | … |
温度y/℃ | … | ﹣20 | ﹣10 | ﹣8 | ﹣5 | ﹣4 | ﹣8 | ﹣12 | ﹣16 | ﹣20 | ﹣10 | ﹣8 | ﹣5 | ﹣4 | a | ﹣20 | … |
(1)通过分析发现,冷柜中的温度y是时间x的函数.
①当4≤x<20时,写出一个符合表中数据的函数解析式 ;
②当20≤x<24时,写出一个符合表中数据的函数解析式 ;
(2)温度不低于﹣8℃的持续时间为 min;
(3)A的值为 .
【答案】(1)①y=﹣![]() ;②y=﹣4x+76(2)11;(3)﹣12
;②y=﹣4x+76(2)11;(3)﹣12
【解析】试题分析:(1)①由xy=-80,即可得出当4≤x<20时,y关于x的函数解析式;
②根据点(20,-4)、(21,-8),利用待定系数法求出y关于x的函数解析式,再代入其它点的坐标验证即可;
(2)观察表格可知,10≤x≤21时,y≥-8,即可求解;
(3)根据表格数据,找出冷柜的工作周期为20分钟,由此即可得出a值.
试题解析:
(1)①∵4×(﹣20)=﹣80,8×(﹣10)=﹣80,10×(﹣8)=﹣80,16×(﹣5)=﹣80,
∴当4≤x<20时,y=﹣![]() .
.
故答案为:y=﹣![]() ;
;
②当20≤x<24时,设y关于x的函数解析式为y=kx+b,
将(20,﹣4)、(21,﹣8)代入y=kx+b中,
![]() ,解得:
,解得: ![]() ,
,
∴此时y=﹣4x+76.
当x=22时,y=﹣4x+76=﹣12,
当x=23时,y=﹣4x+76=﹣16,
当x=24时,y=﹣4x+76=﹣20.
∴当20≤x<24时,y=﹣4x+76.
故答案为:y=﹣4x+76.
(2)由表格可知,10≤x≤21时,y≥﹣8,
则温度不低于﹣8℃的持续时间为21﹣10=11分钟.
故答案为11;
(3)观察表格,可知该冷柜的工作周期为20分钟,
∴当x=42时,与x=22时,y值相同,
∴a=﹣12.
故答案为:﹣12.


科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里.
﹣4,﹣|﹣![]() |,0,
|,0,![]() ,﹣3.14,2019,﹣(+5),+1.88,
,﹣3.14,2019,﹣(+5),+1.88,
(1)正数集合:{ _____…};(2)负数集合:{__________…};
(3)分数集合:{_______…};(4)非负整数集合:{_______…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对七年级全体学生进行了期中测试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了下面的条形图和扇形图(图1和图2均不完整)请根据图中所给的信息,解答下列问题:
(1)求抽取学生的人数,请将表示成绩类别为“中”的条形图补充完整;
(2)求扇形图中表示成绩类别为“优“的扇形所占的百分数;
(3)如果该校七年级共有300人参加期中测试,请估计成绩在“良”及“良”以上的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与x轴交于A,B两点,与y轴交于点C,顶点为D,点C’是点C关于对称轴的对称点,过点D作DG⊥x轴交x轴于点G,交线段AC于点E。
与x轴交于A,B两点,与y轴交于点C,顶点为D,点C’是点C关于对称轴的对称点,过点D作DG⊥x轴交x轴于点G,交线段AC于点E。
(1)连接DC,求△DCE的周长;
(2)如图2,点P是线段AC上方抛物线上的一点,过P作PH⊥x 轴交x轴于点H,交线段AC于点Q,当四边形PCQC’的面积最大时,在线段PH上有一动点M,在线段DG上有一动点N,在y轴上有一动点E,且满足MN⊥PH,连接AM,MN,NE,DE,求AM+MN+NE+DE的最小值;
(3)如图3,将抛物线沿直线AC进行平移,平移过程中的点D记为D’,点C记为C’,连接D’C’所形成的直线与x轴相交于点G,请问是否存在这样的点G,使得△D’OG为等腰三角形?若存在,求出此时OG的长度,若不存在,请说明理由。


图1 图2
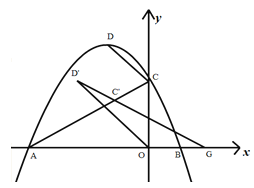
图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,某超市对出售![]() 、
、![]() 两种商品开展元旦促销活动,活动方案有如下两种:(同一种商品不可同时参与两种活动)
两种商品开展元旦促销活动,活动方案有如下两种:(同一种商品不可同时参与两种活动)
商品 |
|
| |
标价(单位:元) |
|
| |
方案一 | 每件商品出售价格 | 按标价降价 | 按标价降价 |
方案二 | 若所购商品超过 | ||
(1)某单位购买![]() 商品
商品![]() 件,
件,![]() 商品
商品![]() 件,共花费
件,共花费![]() 元,试求
元,试求![]() 的值;
的值;
(2)在(1)求出的![]() 值的条件下,若某单位购买
值的条件下,若某单位购买![]() 商品
商品![]() 件(
件(![]() 为正整数),购买
为正整数),购买![]() 商品的件数比
商品的件数比![]() 商品件数的
商品件数的![]() 倍还多一件,请问该单位选择哪种方案才能获得最大优惠?请说明理由.
倍还多一件,请问该单位选择哪种方案才能获得最大优惠?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是关于
是关于![]() 的二次多项式,且二次项系数和一次项系数分别为
的二次多项式,且二次项系数和一次项系数分别为![]() 和
和![]() ,在数轴上
,在数轴上![]() 、
、![]() 、
、![]() 三点所对应的数分别是
三点所对应的数分别是![]() 、
、![]() 、
、![]() .
.
![]()
(1)有一动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度向左运动,多少秒后,
个单位的速度向左运动,多少秒后,![]() 到
到![]() 、
、![]() 、
、![]() 的距离和为
的距离和为![]() 个单位?
个单位?
(2)在(1)的条件下,当点![]() 移动到点
移动到点![]() 时立即掉头,速度不变,同时点
时立即掉头,速度不变,同时点![]() 和点
和点![]() 分别从点
分别从点![]() 和点
和点![]() 出发,向右运动,点
出发,向右运动,点![]() 的速度
的速度![]() 个单位
个单位![]() 秒,点
秒,点![]() 的速度
的速度![]() 个单位
个单位![]() 秒.设点
秒.设点![]() 、
、![]() 、
、![]() 所对应的数分别是
所对应的数分别是![]() 、
、![]() 、
、![]() ,点
,点![]() 出发的时间为
出发的时间为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=10,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,AG=2.5,则△CEF的周长为

查看答案和解析>>
科目:初中数学 来源: 题型:
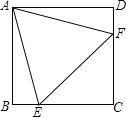
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=![]() .
.
其中正确的序号是 (把你认为正确的都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:

A. A→O→B B. B→A→C C. B→O→C D. C→B→O
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com