
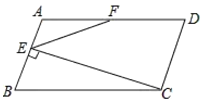
【题目】如图,在平行四边形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 于
于![]() ,设
,设![]() .
.
(1)当![]() 时,求
时,求![]() 的长
的长
(2)当![]() 时,
时,
①求证:![]()
②当![]() 取得最大值时,求
取得最大值时,求![]() 的值.
的值.
【答案】(1)![]() ;(2)①详见解析;②
;(2)①详见解析;②![]()
【解析】
(1)直接运用三角函数的定义构建方程,解答即可;
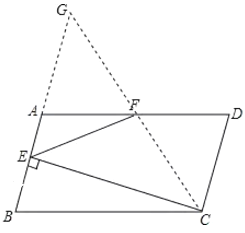
(2)①连接CF并交BA延长交的延长线于点G,先利用中点的定义和平行四边形的性质说明![]() ,然后利用全等三角形的性质、等腰三角形的性质等知识即可解答;
,然后利用全等三角形的性质、等腰三角形的性质等知识即可解答;
②连接CF,并延长交BA的延长线于点G,设![]() ,再由勾股定理得到
,再由勾股定理得到![]() ,进一步得到
,进一步得到![]() ,然后求出CE和最大值,最后利用正弦的定义解答即可.
,然后求出CE和最大值,最后利用正弦的定义解答即可.
解:(1)在直角![]() 中,
中,![]()
![]()
(2)①连接CF并交BA延长交的延长线于点G,
∵F为AD的中点,
![]()
在平行四边形![]() 中,
中,![]()
![]()
在![]() 和
和![]() 中,
中,
![]() ,
,![]()
![]()
![]()
![]() 是边GC中点.
是边GC中点.
![]()
![]()
![]() 是AD的中点,
是AD的中点,
![]()
![]()
在![]() 中,
中,![]()
又![]()
![]()
![]()
②连接CF,并延长交BA的延长线于点G,
设![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]()
![]()
![]() (①中已证)
(①中已证)
![]()
![]()
当![]() ,即点E是AB的中点时,
,即点E是AB的中点时,![]() 取最大值,
取最大值,
所以![]()
![]()


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
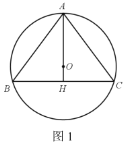
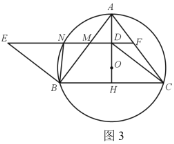
【题目】如图1,已知,⊙O是△ABC的外接圆,AB=AC=10,BC=12,连接AO并延长交BC于点H.
(1)求外接圆⊙O的半径;
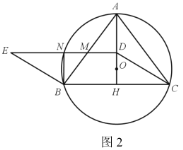
(2)如图2,点D是AH上(不与点A,H重合)的动点,以CD,CB为边,作平行四边形CDEB,DE分别交⊙O于点N,交AB边于点M.
①连接BN,当BN⊥DE时,求AM的值;
②如图3,延长ED交AC于点F,求证:NM·NF=AM·MB;
③设AM=x,要使![]() -2
-2![]() <0成立,求x的取值范围.
<0成立,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
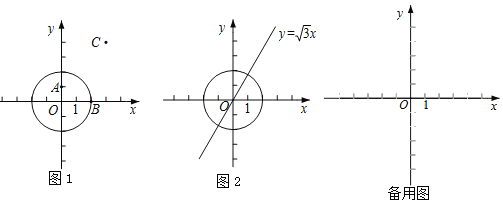
【题目】对于平面直角坐标系xOy中的点P和⊙M(半径为r),给出如下定义:若点P关于点M的对称点为Q,且r≤PQ≤3r,则称点P为⊙M的称心点.
(1)当⊙O的半径为2时,
①如图1,在点A(0,1),B(2,0),C(3,4)中,⊙O的称心点是 ;
②如图2,点D在直线y![]() x上,若点D是⊙O的称心点,求点D的横坐标m的取值范围;
x上,若点D是⊙O的称心点,求点D的横坐标m的取值范围;
(2)⊙T的圆心为T(0,t),半径为2,直线y![]() x+1与x轴,y轴分别交于点E,F.若线段EF上的所有点都是⊙T的称心点,直接写出t的取值范围.
x+1与x轴,y轴分别交于点E,F.若线段EF上的所有点都是⊙T的称心点,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本);并求出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=-x2+(m-1) x+m (m为常数),其顶点为M.
(1)请判断该函数的图像与x轴公共点的个数,并说明理由;
(2)当-2≤m≤3时,求该函数的图像的顶点M纵坐标的取值范围;
(3)在同一坐标系内两点A(-1,-1)、B(1,0),△ABM的面积为S,当m为何值时,S的面积最小?并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步深化基教育课程改革,构建符合素质教育要求的学校课程体系,某学校自主开发了A书法、B阅读,C足球,D器乐四门校本选修课程供学生选择,每门课程被选到的机会均等.
(1)学生小红计划选修两门课程,请写出所有可能的选法;
(2)若学生小明和小刚各计划送修一门课程,则他们两人恰好选修同一门课程的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】碑林书法社小组用的书法练习纸(毛边纸可以到甲商店购买,也可以到乙商店购买已知两商店的标价都是每刀20元(每刀100张),但甲商店的优惠条件是:若购买不超过10刀,则按标价买,购买10以上,从第11刀开始按标价的七折卖;乙商店的优惠条件是:购买一只9元的毛笔,从第一刀开始按标价的八五折卖.购买刀数为![]() (刀),在甲商店购买所需费用为
(刀),在甲商店购买所需费用为![]() 元,在乙商店购买所需费用为
元,在乙商店购买所需费用为![]() 元.
元.
(1)写出![]() 、
、![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)求在乙商店购买所需总费用小于甲商店购买所需总费用时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在歌唱比赛中,一位歌手分别转动如下的两个转盘(每个转盘都被分成3等份)一次,根据指针指向的歌曲名演唱两首曲目.
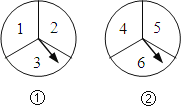
(1)转动转盘①时,该转盘指针指向歌曲“3”的概率是 ;
(2)若允许该歌手替换他最不擅长的歌曲“3”,即指针指向歌曲“3”时,该歌手就选择自己最擅长的歌曲“1”, 请用树形图或列表法中的一种,求他演唱歌曲“1”和“4”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com