
【题目】如图,矩形![]() 中,
中,![]() 对角线
对角线![]() 交于点
交于点![]() 为
为![]() 上任意点,
上任意点,![]() 为
为![]() 中点,则
中点,则![]() 的最小值为( )
的最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
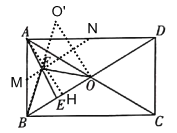
设M、N分别为AB、AD的中点,则MN是△ABD的中位线,点F在MN上,作点O关于MN的对称点O′,连接BO′,则BO′即为![]() 的最小值,易证△ABO是等边三角形,过点A作AH⊥BO于H,求出AH=OO′=
的最小值,易证△ABO是等边三角形,过点A作AH⊥BO于H,求出AH=OO′=![]() ,然后利用勾股定理求出BO′即可.
,然后利用勾股定理求出BO′即可.
解:如图,设M、N分别为AB、AD的中点,则MN是△ABD的中位线,
∵E为BD上任意点,F为AE中点,
∴点F在MN上,
作点O关于MN的对称点O′,连接BO′,则BO′即为![]() 的最小值,
的最小值,
∵四边形ABCD是矩形,![]() ,
,
∴OA=OB,∠AOB=60°,
∴△ABO是等边三角形,
∴AB=BO=4,
过点A作AH⊥BO于H,则BH=HO=2,
∴AH=![]() ,
,
∵MN∥BD,点H关于MN的对称点为A,点O关于MN的对称点为O′
∴OO′=AH=![]() ,且OO′⊥BD,
,且OO′⊥BD,
∴![]() ,
,
即![]() 的最小值为
的最小值为![]() ,
,
故选:A.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
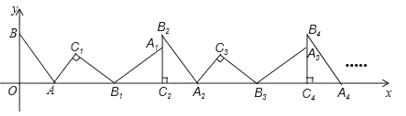
【题目】如图,在平面直角坐标系中,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() ,
,![]() 分别落在点
分别落在点![]() ,
,![]() 处,点
处,点![]() 在
在![]() 轴上,再将
轴上,再将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 轴上,将
轴上,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 轴上,依次进行下去……,若点
轴上,依次进行下去……,若点![]() ,
,![]() ,则点
,则点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.

(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
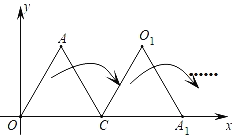
【题目】如图,已知点A在第一象限,点C的坐标为(1,0),△AOC是等边三角形,现把△AOC按如下规律进行旋转:第1次旋转,把△AOC绕点C按顺时针方向旋转120°后得到△A1O1C,点A1、O1分别是点A、O的对应点,第2次旋转,把△A1O1C绕着点A1按顺时针方向旋转120°后得到△A1O2C1,点O2、C1分别是点O1、C的对应点,第3次旋转,把△A1O2C1绕着点O2按顺时针方向旋转120°后得到△A2O2C2,点A2、C2分别是点A1、C1的对应点,……,依此规律,第6次旋转,把△A3O4C3绕着点O4按顺时针方向旋转120°后得到△A4O4C4,点A4、C4分别是点A3、C3的对应点,则点A4的坐标是( )
A.(![]() ,
,![]() )B.(6,0)C.(
)B.(6,0)C.(![]() ,
,![]() )D.(7,0)
)D.(7,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
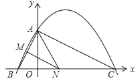
【题目】如图,已知二次函数y=ax2+![]() x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)求出二次函数表达式;
(2)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请求出此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】孙老师在上《等可能事件的概率》这节课时,给同学们提出了一个问题:“如果同时随机投掷两枚质地均匀的骰子,它们朝上一面的点数和是多少的可能性最大?”同学们展开讨论,各抒己见,其中小芳和小超两位同学给出了两种不同的回答.小芳认为6的可能性最大,小超认为7的可能性最大.你认为他们俩的回答正确吗?请用列表或画树状图等方法加以说明.(骰子:六个面上分别刻有1,2,3,4,5,6个小圆点的小正方体.)
查看答案和解析>>
科目:初中数学 来源: 题型:
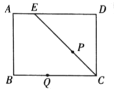
【题目】如图,在矩形![]() 中,
中,![]() 为
为![]() 上一点,且
上一点,且![]() ,
,![]() ,点
,点![]() ,
,![]() 同时从
同时从![]() 点出发,点
点出发,点![]() 以每秒
以每秒![]() 的速度沿
的速度沿![]() 向终点
向终点![]() 运动,点
运动,点![]() 以每秒2的速度沿折线
以每秒2的速度沿折线![]() 向终点
向终点![]() 运动,设
运动,设![]() 运动的时间为
运动的时间为![]() ,
,![]() ,
,![]() 经过的路线与
经过的路线与![]() 围成的图形面积为
围成的图形面积为![]() ,则
,则![]() 关于
关于![]() 的图象大致是( )
的图象大致是( )
A.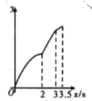 B.
B.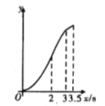 C.
C. D.
D.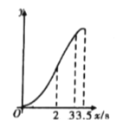
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com