
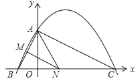
【题目】如图,已知二次函数y=ax2+![]() x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)求出二次函数表达式;
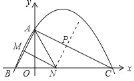
(2)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请求出此时点N的坐标.
【答案】(1) y=﹣![]() x2+
x2+![]() x+4;(2) (3,0);(3)N(﹣8,0)、(8﹣4
x+4;(2) (3,0);(3)N(﹣8,0)、(8﹣4![]() ,0)、(3,0)、(8+4
,0)、(3,0)、(8+4![]() ,0).
,0).
【解析】
(1)根据待定系数法即可求得;
(2)设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,根据三角形相似对应边成比例求得MD=![]() (n+2),构建二次函数,根据函数解析式求得即可;
(n+2),构建二次函数,根据函数解析式求得即可;
(3)分别以A、C两点为圆心,AC长为半径画弧,与x轴交于三个点,由AC的垂直平分线与x轴交于一个点,即可求得点N的坐标.
解:(1)∵二次函数y=ax2+![]() x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),
x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),
∴![]() ,
,
解得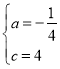 .
.
∴抛物线表达式:![]() ;
;![]()
(2)令y=0,则![]() ,
,
解得x1=8,x2=﹣2,
∴点B的坐标为(﹣2,0).
又∵A(0,4),C(8,0),
∴![]() ,
,
∴AB2+AC2=BC2,
∴∠BAC=90°.
∴AC⊥AB.
∵AC∥MN,
∴MN⊥AB.
设点N的坐标为(n,0),则BN=n+2,
∵MN∥AC,
△BMN∽△BAC
∴![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
∵S△AMN=![]() AMMN
AMMN
=![]()
=![]() ,
,
当n=3时,△AMN面积最大是5,
∴N点坐标为(3,0).
∴当△AMN面积最大时,N点坐标为(3,0).
(3)由(2)知,AC=![]() ,
,
①以A为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(﹣8,0),
②以C为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(![]() ,0)或(
,0)或(![]() ,0)
,0)
③作AC的垂直平分线交AC于P,交x轴于N,
∴△AOC∽△NPC.
∴![]() 即
即![]() .
.
∴CN=5.
∴此时N的坐标为(3,0),
综上,若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(﹣8,0)、(![]() ,0)、(3,0)、(
,0)、(3,0)、(![]() ,0).
,0).


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】已知函数y=-x2+(m-1) x+m (m为常数),其顶点为M.
(1)请判断该函数的图像与x轴公共点的个数,并说明理由;
(2)当-2≤m≤3时,求该函数的图像的顶点M纵坐标的取值范围;
(3)在同一坐标系内两点A(-1,-1)、B(1,0),△ABM的面积为S,当m为何值时,S的面积最小?并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到.若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=![]() HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.
HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】碑林书法社小组用的书法练习纸(毛边纸可以到甲商店购买,也可以到乙商店购买已知两商店的标价都是每刀20元(每刀100张),但甲商店的优惠条件是:若购买不超过10刀,则按标价买,购买10以上,从第11刀开始按标价的七折卖;乙商店的优惠条件是:购买一只9元的毛笔,从第一刀开始按标价的八五折卖.购买刀数为![]() (刀),在甲商店购买所需费用为
(刀),在甲商店购买所需费用为![]() 元,在乙商店购买所需费用为
元,在乙商店购买所需费用为![]() 元.
元.
(1)写出![]() 、
、![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)求在乙商店购买所需总费用小于甲商店购买所需总费用时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线M:y=- ![]() x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M'.若抛物线M'与x轴交于A、B两点,M'的顶点记为C,则∠ACB=( )
x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M'.若抛物线M'与x轴交于A、B两点,M'的顶点记为C,则∠ACB=( )
A.45°B.60°C.90°D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
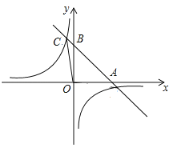
【题目】如图,直线![]() 经过点A(3,0)和点B(0,2).
经过点A(3,0)和点B(0,2).
(1)求直线![]() 的解析式;
的解析式;
(2)直线![]() 与函数
与函数![]() 的图象交于点C(C在第二象限),若ΔCOB的面积与ΔAOB的面积相等,求出m的值.
的图象交于点C(C在第二象限),若ΔCOB的面积与ΔAOB的面积相等,求出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 内接于
内接于![]() ,
,![]() ,连接
,连接![]() ;
;
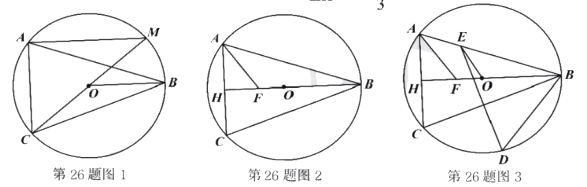
(1)如图1,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(2)如图2,延长![]() 交
交![]() 于点H,点F为BH上一点,连接AF,若
于点H,点F为BH上一点,连接AF,若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,如图3,点E为AB上一点,点D为![]() 上一点,连接
上一点,连接![]() 、
、![]() ,若
,若![]() ,若
,若![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com