
【题目】![]() 内接于
内接于![]() ,
,![]() ,连接
,连接![]() ;
;
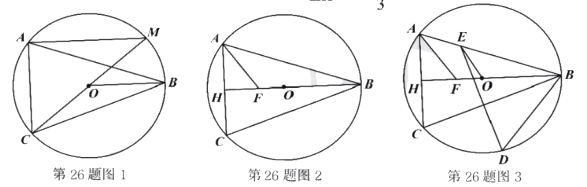
(1)如图1,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
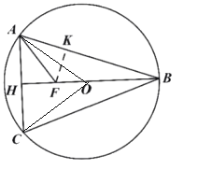
(2)如图2,延长![]() 交
交![]() 于点H,点F为BH上一点,连接AF,若
于点H,点F为BH上一点,连接AF,若![]() ,求证:
,求证:![]() ;
;
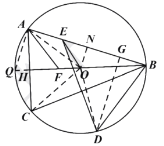
(3)在(2)的条件下,如图3,点E为AB上一点,点D为![]() 上一点,连接
上一点,连接![]() 、
、![]() ,若
,若![]() ,若
,若![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)根据![]() =
=![]() 得到
得到![]() ,再证明
,再证明![]() 即可得到答案;
即可得到答案;
(2)过点![]() 作
作![]() ,连接
,连接![]() 、
、![]() ,证明
,证明![]() 平分
平分![]() 即可得到答案;
即可得到答案;
(3)延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,先求
,先求![]() ,再根据
,再根据![]() 求出
求出![]() ,再利用勾股定理即可得到答案;
,再利用勾股定理即可得到答案;
(1)∵![]() =
=![]()
∴![]() (同弧所对圆周角相等),
(同弧所对圆周角相等),
∵![]() 为直径,
为直径,
∴![]() (直径所对的角是90°)
(直径所对的角是90°)
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]() (内错角相等,两直线平行),
(内错角相等,两直线平行),
(2)过点![]() 作
作![]() ,连接
,连接![]() 、
、![]()
∵![]()
∴点![]() 在
在![]() 的垂直平分线上
的垂直平分线上
∵![]()
∴点![]() 在
在![]() 的垂直平分线上
的垂直平分线上
∴![]() 垂直平分
垂直平分![]()
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 平分
平分![]() ,
,
∴![]() ,
,
(3)延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
∵![]() ,
,![]()
∴![]()
∵![]()
![]()
∴![]() (同弧所对的圆周角相等),
(同弧所对的圆周角相等),
∴![]()
![]()
∴![]()
∴![]()
设半径为![]() ,则
,则![]() ,
,![]()
∴![]()
即![]()
解得![]() 或
或![]() (舍去)
(舍去)
∴![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
∴![]() ,
,![]() ,
,![]()
∵![]()
![]()
![]()
∴![]()
连接![]() 、
、![]()
∴![]()
∴![]()
∴![]()
过点![]() 作
作![]() 于
于![]() ,如上图,
,如上图,
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
过![]() 作
作![]() 于
于![]() ,如上图,
,如上图,
∴![]()
∴![]()
∵![]()
∴![]()
∴![]() ,
,


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
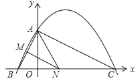
【题目】如图,已知二次函数y=ax2+![]() x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)求出二次函数表达式;
(2)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请求出此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,连接
上一点,连接![]()
(1)如图1,若![]() ,
,![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 与
与![]() 垂直,求证:
垂直,求证:![]()
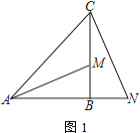
(2)过点![]() 作
作![]() ,
,![]() 为垂足,连接
为垂足,连接![]() 并延长交
并延长交![]() 于点
于点![]() .
.
①如图2,若![]() ,求证:
,求证:![]()
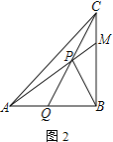
②如图3,若![]() 是
是![]() 的中点,直接写出
的中点,直接写出![]() 的值(用含
的值(用含![]() 的式子表示)
的式子表示)
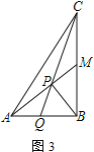
查看答案和解析>>
科目:初中数学 来源: 题型:
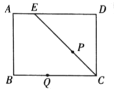
【题目】如图,在矩形![]() 中,
中,![]() 为
为![]() 上一点,且
上一点,且![]() ,
,![]() ,点
,点![]() ,
,![]() 同时从
同时从![]() 点出发,点
点出发,点![]() 以每秒
以每秒![]() 的速度沿
的速度沿![]() 向终点
向终点![]() 运动,点
运动,点![]() 以每秒2的速度沿折线
以每秒2的速度沿折线![]() 向终点
向终点![]() 运动,设
运动,设![]() 运动的时间为
运动的时间为![]() ,
,![]() ,
,![]() 经过的路线与
经过的路线与![]() 围成的图形面积为
围成的图形面积为![]() ,则
,则![]() 关于
关于![]() 的图象大致是( )
的图象大致是( )
A.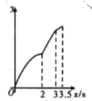 B.
B.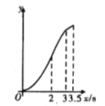 C.
C. D.
D.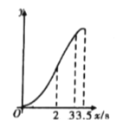
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
![]() 纸是我们学习工作最常用的纸张之一, 其长宽之比是
纸是我们学习工作最常用的纸张之一, 其长宽之比是![]() ,我们定义:长宽之比是
,我们定义:长宽之比是![]() 的矩形纸片称为“标准纸”.
的矩形纸片称为“标准纸”.
操作判断:
![]() 如图1所示,矩形纸片
如图1所示,矩形纸片![]() 是一张“标准纸”,将纸片折叠一次,使点
是一张“标准纸”,将纸片折叠一次,使点![]() 与
与![]() 重合,再展开,折痕
重合,再展开,折痕![]() 交
交![]() 边于点
边于点![]() 交
交![]() 边于点
边于点![]() ,若
,若![]() 求
求![]() 的长,
的长,
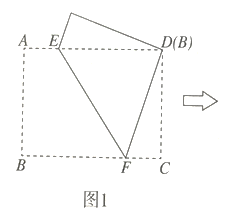
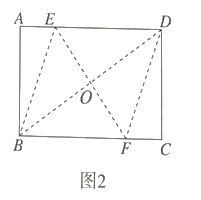
![]() 如图2,在
如图2,在![]() 的基础上,连接
的基础上,连接![]() 折痕
折痕![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 判断四边形
判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
探究发现:
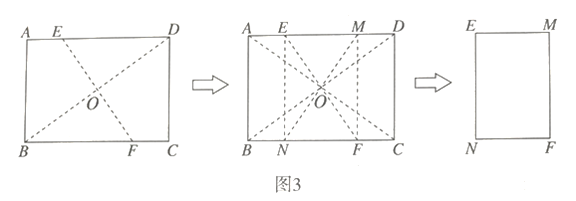
![]() 如图3所示,在(1)和(2)的基础上,展开纸片后,将纸片再折叠一次,使点
如图3所示,在(1)和(2)的基础上,展开纸片后,将纸片再折叠一次,使点![]() 与点
与点![]() 重合,再展开,痕
重合,再展开,痕![]() 交
交![]() 边于点
边于点![]() ,
,![]() 交边于点
交边于点![]() 交
交![]() 也是点
也是点![]() .然后将四边形
.然后将四边形![]() 剪下,探究纸片
剪下,探究纸片![]() 是否为“标准纸”,说明理由.
是否为“标准纸”,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1和图2,矩形ABCD中,E是AD的中点,P是BC上一点,AF∥PD,∠FPE=∠DPE.
(1)作射线PE交直线AF于点G,如图1.
①求证:AG=DP;
②若点F在AD下方,AF=2,PF=7,求DP的长.
(2)若点F在AD上方,如图2,直接写出PD,AF,PF的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组
请结合题意填空,完成本题的解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在数轴上表示出来:
![]()
(4)原不等式维的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展征文活动,征文主题只能从“爱国”、“敬业”、“诚信”、“友善”四个主题中选择一个,每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)将上面的条形统计图补充完整;
(2)在扇形统计图中,选择“爱国”主题所对应的圆心角是_____度;
(3)如果该校七年级共有1200名考生,请估计选择以“友善”为主题的七年级学生有______名;
(4)学生会宣传部有七年级的2名男生和2名女生,现从中随机挑选2名同学参加“主题征文”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com