
【题目】综合与实践
![]() 纸是我们学习工作最常用的纸张之一, 其长宽之比是
纸是我们学习工作最常用的纸张之一, 其长宽之比是![]() ,我们定义:长宽之比是
,我们定义:长宽之比是![]() 的矩形纸片称为“标准纸”.
的矩形纸片称为“标准纸”.
操作判断:
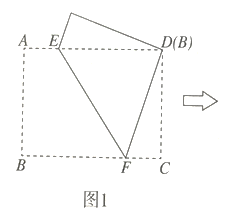
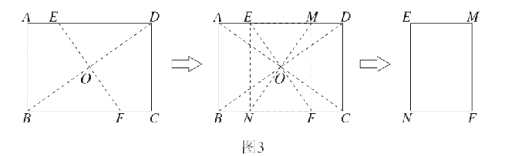
![]() 如图1所示,矩形纸片
如图1所示,矩形纸片![]() 是一张“标准纸”,将纸片折叠一次,使点
是一张“标准纸”,将纸片折叠一次,使点![]() 与
与![]() 重合,再展开,折痕
重合,再展开,折痕![]() 交
交![]() 边于点
边于点![]() 交
交![]() 边于点
边于点![]() ,若
,若![]() 求
求![]() 的长,
的长,
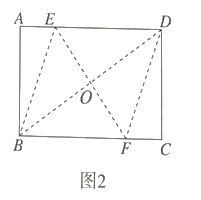
![]() 如图2,在
如图2,在![]() 的基础上,连接
的基础上,连接![]() 折痕
折痕![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 判断四边形
判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
探究发现:
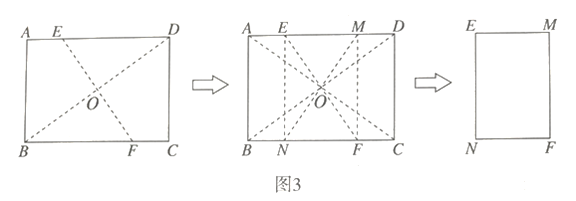
![]() 如图3所示,在(1)和(2)的基础上,展开纸片后,将纸片再折叠一次,使点
如图3所示,在(1)和(2)的基础上,展开纸片后,将纸片再折叠一次,使点![]() 与点
与点![]() 重合,再展开,痕
重合,再展开,痕![]() 交
交![]() 边于点
边于点![]() ,
,![]() 交边于点
交边于点![]() 交
交![]() 也是点
也是点![]() .然后将四边形
.然后将四边形![]() 剪下,探究纸片
剪下,探究纸片![]() 是否为“标准纸”,说明理由.
是否为“标准纸”,说明理由.
【答案】(1) ![]() 长为
长为![]() ;(2) 四边形
;(2) 四边形![]() 是菱形,理由见解析;(3) 纸片
是菱形,理由见解析;(3) 纸片![]() 是“标准纸",理由见解析
是“标准纸",理由见解析
【解析】
(1)![]() ,则
,则![]() ,根据四边形
,根据四边形![]() 是矩形,得到
是矩形,得到![]() ,由折叠得
,由折叠得![]() ,设
,设![]() ,则
,则![]() ,在
,在![]() 中,
中,![]() ,可得
,可得![]() 即可求解.
即可求解.
(2)当顶点![]() 与点
与点![]() 重合时,折痕
重合时,折痕![]() 垂直平分
垂直平分![]() ,可得
,可得![]() ,
,![]() ,在矩形
,在矩形![]() 中,
中,![]() ,得到
,得到![]() ,在
,在![]() 和
和![]() 中,
中,![]() ,可得
,可得![]() ,
,![]() ,再根据
,再根据![]() ,可得四边形
,可得四边形![]() 是平行四边形,最后根据
是平行四边形,最后根据![]() ,即可求证平行四边形
,即可求证平行四边形![]() 是菱形.
是菱形.
(3)由![]() 可知,
可知,![]() ,同理可知,
,同理可知,![]() ,可得四边形
,可得四边形![]() 是平行四边形,根据
是平行四边形,根据![]() ,得到
,得到![]() ,再根据
,再根据![]() ,可得
,可得![]() ,进而得到
,进而得到![]() ,
,![]() ,同理可得,
,同理可得,![]() ,根据四边形
,根据四边形![]() 是矩形,可得
是矩形,可得![]() ,
,![]() ,四边形
,四边形![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() ,即可求证纸片
,即可求证纸片![]() 是“标准纸".
是“标准纸".
解:![]() 则
则![]()
![]() 四边形
四边形![]() 是矩形
是矩形
![]()
由折叠得![]()
设![]() ,则
,则![]()
在![]() 中,
中,![]()
![]()
![]()
答:![]() 长为
长为![]()
![]() 四边形
四边形![]() 是菱形.
是菱形.
理由:当顶点![]() 与点
与点![]() 重合时,折痕
重合时,折痕![]() 垂直平分
垂直平分![]()
![]() ,
,![]()
在矩形![]() 中,
中,![]()
![]()
在![]() 和
和![]() 中,
中,![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]()
平行四边形![]() 是菱形.
是菱形.
![]() 纸片
纸片![]() 是“标准纸”
是“标准纸”
理由如下:由![]() 可知,
可知,![]()
同理可知,![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]()
![]()
![]()
![]()
![]()
![]()
同理可得,![]()
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]()
![]() 四边形
四边形![]() 是矩形.
是矩形.
![]() .
.
![]()
![]() .
.
![]() 纸片
纸片![]() 是“标准纸".
是“标准纸".


科目:初中数学 来源: 题型:
【题目】碑林书法社小组用的书法练习纸(毛边纸可以到甲商店购买,也可以到乙商店购买已知两商店的标价都是每刀20元(每刀100张),但甲商店的优惠条件是:若购买不超过10刀,则按标价买,购买10以上,从第11刀开始按标价的七折卖;乙商店的优惠条件是:购买一只9元的毛笔,从第一刀开始按标价的八五折卖.购买刀数为![]() (刀),在甲商店购买所需费用为
(刀),在甲商店购买所需费用为![]() 元,在乙商店购买所需费用为
元,在乙商店购买所需费用为![]() 元.
元.
(1)写出![]() 、
、![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)求在乙商店购买所需总费用小于甲商店购买所需总费用时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在歌唱比赛中,一位歌手分别转动如下的两个转盘(每个转盘都被分成3等份)一次,根据指针指向的歌曲名演唱两首曲目.
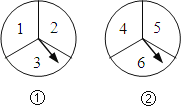
(1)转动转盘①时,该转盘指针指向歌曲“3”的概率是 ;
(2)若允许该歌手替换他最不擅长的歌曲“3”,即指针指向歌曲“3”时,该歌手就选择自己最擅长的歌曲“1”, 请用树形图或列表法中的一种,求他演唱歌曲“1”和“4”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() .
.
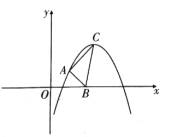
(1)求![]() ,
,![]() 的值;
的值;
(2)已知![]() 点为抛物线上异于
点为抛物线上异于![]() 的一点,且
的一点,且![]() 点横、纵坐标相等,
点横、纵坐标相等,![]() 为
为![]() 轴上任意一点,当
轴上任意一点,当![]() 取最小值时,求出
取最小值时,求出![]() 点坐标和此时
点坐标和此时![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 内接于
内接于![]() ,
,![]() ,连接
,连接![]() ;
;
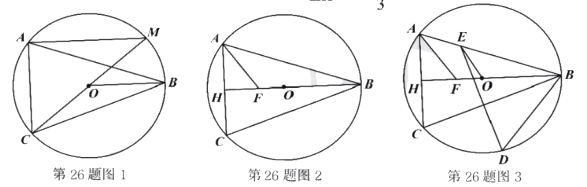
(1)如图1,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(2)如图2,延长![]() 交
交![]() 于点H,点F为BH上一点,连接AF,若
于点H,点F为BH上一点,连接AF,若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,如图3,点E为AB上一点,点D为![]() 上一点,连接
上一点,连接![]() 、
、![]() ,若
,若![]() ,若
,若![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,给定一个正方形,要通过画线将其分割成若干个互不重叠的正方形.第1次画线分割成4个互不重叠的正方形,得到图2;第2次画线分割成7个互不重叠的正方形,得到图3……以后每次只在上次得到图形的左上角的正方形中画线.
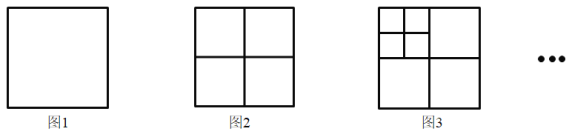
尝试:第3次画线后,分割成 个互不重叠的正方形;
第4次画线后,分割成 个互不重叠的正方形.
发现:第n次画线后,分割成 个互不重叠的正方形;并求第2020次画线后得到互不重叠的正方形的个数.
探究:若干次画线后,能否得到1001个互不重叠的正方形?若能,求出是第几次画线后得到的;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴是
的对称轴是![]() .且过点(
.且过点(![]() ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④2c-3b>0;⑤a﹣b≥m(am﹣b)(m≠-1);其中所有正确的结论是( )
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④2c-3b>0;⑤a﹣b≥m(am﹣b)(m≠-1);其中所有正确的结论是( )
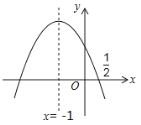
A.①②③B.①③④C.①③④⑤D.②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是正方形,点
是正方形,点![]() 的坐标是
的坐标是![]() .
.
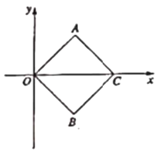
(1)正方形![]() 的边长为 ,点
的边长为 ,点![]() 的坐标是 ;
的坐标是 ;
(2)将正方形![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() ,
,![]() ,
,![]() 旋转后的对应点为
旋转后的对应点为![]() ,
,![]() ,
,![]() ,求点
,求点![]() 的坐标及旋转后的正方形与原正方形的重叠部分的面积;
的坐标及旋转后的正方形与原正方形的重叠部分的面积;
(3)动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 方向以1个单位/秒的速度匀速运动,同时,另一动点
方向以1个单位/秒的速度匀速运动,同时,另一动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 方向以2个单位/秒的速度匀速运动,运动时间为
方向以2个单位/秒的速度匀速运动,运动时间为![]() 秒,当它们相遇时同时停止运动,当
秒,当它们相遇时同时停止运动,当![]() 为等腰三角形时,求出
为等腰三角形时,求出![]() 的值(直接写出结果即可).
的值(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
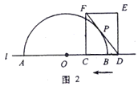
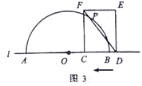
【题目】如图1,点![]() 和矩形
和矩形![]() 的边
的边![]() 都在直线
都在直线![]() 上,以点
上,以点![]() 为圆心,以24为半径作半圆,分别交直线
为圆心,以24为半径作半圆,分别交直线![]() 于
于![]() 两点.已知:
两点.已知: ![]() ,
,![]() ,矩形自右向左在直线
,矩形自右向左在直线![]() 上平移,当点
上平移,当点![]() 到达点
到达点![]() 时,矩形停止运动.在平移过程中,设矩形对角线
时,矩形停止运动.在平移过程中,设矩形对角线![]() 与半圆
与半圆![]() 的交点为
的交点为![]() (点
(点![]() 为半圆上远离点
为半圆上远离点![]() 的交点).
的交点).
(1)如图2,若![]() 与半圆
与半圆![]() 相切,求
相切,求![]() 的值;
的值;
(2)如图3,当![]() 与半圆
与半圆![]() 有两个交点时,求线段
有两个交点时,求线段![]() 的取值范围;
的取值范围;
(3)若线段![]() 的长为20,直接写出此时
的长为20,直接写出此时![]() 的值.
的值.
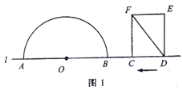
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com