
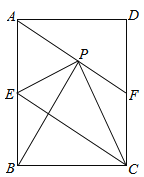
【题目】如图1和图2,矩形ABCD中,E是AD的中点,P是BC上一点,AF∥PD,∠FPE=∠DPE.
(1)作射线PE交直线AF于点G,如图1.
①求证:AG=DP;
②若点F在AD下方,AF=2,PF=7,求DP的长.
(2)若点F在AD上方,如图2,直接写出PD,AF,PF的等量关系.

【答案】(1)①证明见解析;②DP=5;(2)PD=PF+AF.
【解析】
(1)①根据平行线的性质得到∠GAE=∠PDE,∠G=∠DPE.根据全等三角形的性质即可得到结论;
②等量代换得到∠G=∠FPE.求得GF=PF=7,根据线段的和差即可得到结论;
(2)如图2,根据平行线的性质得到∠G=∠DPE,等量代换得到∠G=∠FPG,求得PF=FG,根据全等三角形的性质得到AG=PD,根据线段的和差即可得到结论.
(1)①∵AF∥PD,
∴∠GAE=∠PDE,∠G=∠DPE,
∵E是AD的中点,
∴AE=DE,
∴△AEG≌△DEP,
∴AG=DP;
②∵∠FPE=∠DPE,∠G=∠DPE,
∴∠G=∠FPE,
∴GF=PF=7.
∵AF=2,
∴AG=5.
由①AG=DP,
∴DP=5;
(2)PD=PF+AF,
理由:如图2,
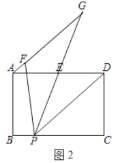
∵AF∥PD,
∴∠G=∠DPE,
∵∠FPE=∠DPE,
∴∠G=∠FPG,
∴PF=FG,
∵∠AEG=∠DEP,AE=DE,
∴△AEG≌△DEP(AAS),
∴AG=PD,
∵AG=AF+FG,
∴PD=AF+PF,
PD=PF+AF.


科目:初中数学 来源: 题型:
【题目】将抛物线M:y=- ![]() x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M'.若抛物线M'与x轴交于A、B两点,M'的顶点记为C,则∠ACB=( )
x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M'.若抛物线M'与x轴交于A、B两点,M'的顶点记为C,则∠ACB=( )
A.45°B.60°C.90°D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在矩形![]() 中,
中,![]() 是对角线,
是对角线,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.

(1)如图1,求证:![]() ;
;
(2)如图2,当![]() 时,连接
时,连接![]() 、
、![]() ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形
,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形![]() 面积的
面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 内接于
内接于![]() ,
,![]() ,连接
,连接![]() ;
;
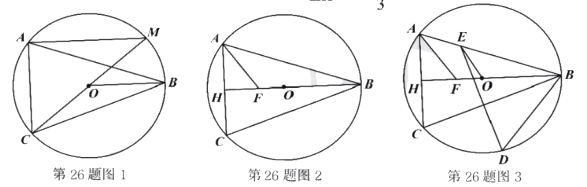
(1)如图1,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(2)如图2,延长![]() 交
交![]() 于点H,点F为BH上一点,连接AF,若
于点H,点F为BH上一点,连接AF,若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,如图3,点E为AB上一点,点D为![]() 上一点,连接
上一点,连接![]() 、
、![]() ,若
,若![]() ,若
,若![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平整的桌面上面一条直线l,将三边都不相等的三角形纸片ABC平放在桌面上,使AC与边l对齐,此时△ABC的内心是点P;将纸片绕点C顺时针旋转,使点B落在l上的点B'处,点A落在A'处,得到△A'B'C'的内心点P'.下列结论正确的是( )
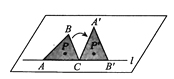
A.PP'与l平行,PC与P'B'平行
B.PP'与l平行,PC与P'B'不平行
C.PP'与l不平行,PC与P'B'平行
D.PP'与l不平行,PC与P'B'不平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴是
的对称轴是![]() .且过点(
.且过点(![]() ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④2c-3b>0;⑤a﹣b≥m(am﹣b)(m≠-1);其中所有正确的结论是( )
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④2c-3b>0;⑤a﹣b≥m(am﹣b)(m≠-1);其中所有正确的结论是( )
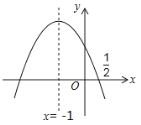
A.①②③B.①③④C.①③④⑤D.②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,
(1)求证:四边形AECF为平行四边形;
(2)若△AEP是等边三角形,连结BP,求证:△APB≌△EPC;
(3)若矩形ABCD的边AB=6,BC=4,求△CPF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区为了加强社区居民对防护新型冠状病毒知识的了解,通过微信宣传防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷,社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据:
甲小区:85 80 95 100 90 95 85 65 75 85
90 90 70 90 100 80 80 90 95 75
乙小区:80 60 80 95 65 100 90 85 85 80
95 75 80 90 70 80 95 75 100 90
整理数据
成绩x(分) | 60≤x≤70 | 70<x≤80 | 80<x≤90 | 90<x≤100 |
甲小区 | 2 | 5 | a | b |
乙小区 | 3 | 7 | 5 | 5 |
分析数据
统计量 | 平均数 | 中位数 | 众数 |
甲小区 | 85.75 | 87.5 | c |
乙小区 | 83.5 | d | 80 |
应用数据
(1)填空:a= ,b= ,c= ,d= ;
(2)根据以上数据, (填“甲”或“乙”)小区对新型冠状病毒肺炎防护知识掌握得更好,理由是 (一条即可).
(3)若甲小区共有800人参加答卷,请估计甲小区成绩高于
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年12月以来,湖北省武汉市发现一种新型冠状病毒感染引起的急性呼吸道传染病.感染者的临床表现为:以发热、乏力、干咳为主要表现.约半数患者多在一周后出现呼吸困难,严重者快速进展为急性呼吸窘迫综合征、脓毒症休克、难以纠正的代谢性酸中毒和出凝血功能障碍.国家卫健委已发布1号公告,将新型冠状病毒感染的肺炎纳入传染病防治法规定的乙类传染病,但采取甲类传染病的预防、控制措施,同时将其纳入检疫传染病管理.
(1)在“新冠”初期,有2人感染了“新冠”,经过两轮传染后共有288人感染了“新冠”(这两轮感染均未被发现未被隔离),则每轮传染中平均一个人传染了几个人?
(2)某小区物管为预防业主感染传播购买![]() 型和
型和![]() 型两种
型两种![]() 口罩,购买
口罩,购买![]() 型
型![]() 口罩花费了2500元,购买
口罩花费了2500元,购买![]() 型
型![]() 口罩花费了2000元,且购买
口罩花费了2000元,且购买![]() 型
型![]() 口罩数量是购买
口罩数量是购买![]() 型
型![]() 口罩数量的2倍,已知购买一个
口罩数量的2倍,已知购买一个![]() 型
型![]() 口罩比购买一个
口罩比购买一个![]() 型
型![]() 口罩多花3元则该物业购买
口罩多花3元则该物业购买![]() 、
、![]() 两种
两种![]() 口罩的单价为多少元?
口罩的单价为多少元?
(3)由于实际需要,该物业决定再次购买这两种![]() 口罩,已知此次购进
口罩,已知此次购进![]() 型和
型和![]() 型两种
型两种![]() 口罩的数量一共为1000个,恰逢市场对这两种
口罩的数量一共为1000个,恰逢市场对这两种![]() 口罩的售价进行调整,
口罩的售价进行调整,![]() 型
型![]() 口罩售价比第一次购买时提高了
口罩售价比第一次购买时提高了![]() ,
,![]() 型
型![]() 口罩按第一次购买时售价的1.5倍出售,如果此次购买
口罩按第一次购买时售价的1.5倍出售,如果此次购买![]() 型和
型和![]() 型这两种
型这两种![]() 口罩的总费用不超过7800元,那么此次最多可购买多少个
口罩的总费用不超过7800元,那么此次最多可购买多少个![]() 型
型![]() 口罩?
口罩?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com