
【题目】(本小题满分9分)如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,
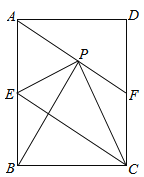
(1)求证:四边形AECF为平行四边形;
(2)若△AEP是等边三角形,连结BP,求证:△APB≌△EPC;
(3)若矩形ABCD的边AB=6,BC=4,求△CPF的面积.
【答案】(1)证明见试题解析;(2)证明见试题解析;(3)![]() .
.
【解析】
试题(1)由折叠的性质得到BE=PE,EC⊥PB,根据E为AB中点,得到AE=PE,利用等角对等边得到两对角相等,利用外角性质得到∠AEP=2∠EPB,设∠EPB=x,则∠AEP=2x,表示出∠APE,由∠APE+∠EPB得到∠APB为90°,进而得到AF与EC平行,再由AE与FC平行,利用两对边平行的四边形为平行四边形即可得证;
(2)根据等边三角形性质,得到△AEP三条边相等,三内角相等,再由折叠的性质及邻补角定义得到一对角相等,根据同角的余角相等得到一对角相等,再由AP=EB,利用AAS即可得证;
(3)过P作PM⊥CD,在Rt△EBC中,利用勾股定理求出EC,利用面积求出BQ,再根据BP=2BQ求出BP,在Rt△ABP中,利用勾股定理求出AP,根据AF-AP求出PF,由PM与AD平行,得到△PMF与△ADF相似,由相似得比例求出PM,再由FC=AE=3,求出△CPF面积即可.
试题解析:(1)由折叠得到BE=PE,EC⊥PB,∵E为AB的中点,∴AE=EB,即AE=PE,∴∠EBP=∠EPB,∠EAP=∠EPA,∵∠AEP为△EBP的外角,∴∠AEP=2∠EPB,设∠EPB=x,则∠AEP=2x,∠APE=![]() =90°﹣x,∴∠APB=∠APE+∠EPB=x+90°﹣x=90°,即BP⊥AF,∴AF∥EC,∵AE∥FC,∴四边形AECF为平行四边形;
=90°﹣x,∴∠APB=∠APE+∠EPB=x+90°﹣x=90°,即BP⊥AF,∴AF∥EC,∵AE∥FC,∴四边形AECF为平行四边形;
(2)∵△AEP为等边三角形,∴∠BAP=∠AEP=60°,AP=AE=EP=EB,∵∠PEC=∠BEC,∴∠PEC=∠BEC=60°,∵∠BAP+∠ABP=90°,∠ABP+∠BEQ=90°,∴∠BAP=∠BEQ,在△ABP和△EBC中,∵∠APB=∠EBC=90°,∠BAP=∠BEQ,AP=EB,∴△ABP≌△EBC(AAS),∵△EBC≌△EPC,∴△ABP≌△EPC;
(3)过P作PM⊥DC,交DC于点M,在Rt△EBC中,EB=3,BC=4,根据勾股定理得:EC=![]() =5,∵S△EBC=
=5,∵S△EBC=![]() EBBC=
EBBC=![]() ECBQ,∴BQ=
ECBQ,∴BQ=![]() =
=![]() ,由折叠得:BP=2BQ=
,由折叠得:BP=2BQ=![]() ,在Rt△ABP中,AB=6,BP=
,在Rt△ABP中,AB=6,BP=![]() ,根据勾股定理得:AP=
,根据勾股定理得:AP=![]() =
=![]() ,∵四边形AECF为平行四边形,∴AF=EC=5,FC=AE=3,∴PF=
,∵四边形AECF为平行四边形,∴AF=EC=5,FC=AE=3,∴PF=![]() =
=![]() ,∵PM∥AD,∴
,∵PM∥AD,∴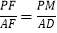 ,即
,即![]() ,解得:PM=
,解得:PM=![]() ,则S△PFC=
,则S△PFC=![]() FCPM=
FCPM=![]() =
=![]() .
.



科目:初中数学 来源: 题型:
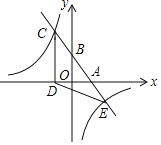
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
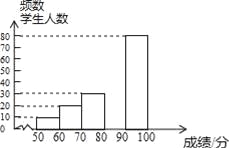
请根据所给信息,解答下列问题:
(1)a=______,b=______;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在_____________分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A:篮球 B:乒乓球C:羽毛球 D:足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:


(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
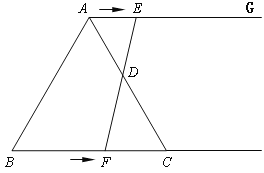
【题目】如图,在等边三角形ABC中,BC=6cm. 射线AG//BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)填空:当t为_________s时,四边形ACFE是菱形;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为菱形ABCD对角线上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点M.
(1)求证:CD与⊙O相切;
(2)若菱形ABCD的边长为2,∠ABC=60°,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.

(1)线段AB,BC,AC的长分别为AB= ,BC= ,AC= ;
(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
请从下列A、B两题中任选一题作答,我选择 题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com