
【题目】某商场甲、乙、丙三名业务员2018年前5个月的销售额(单位:万元)如下表:
月份 销售额 人员 | 第1月 | 第2月 | 第3月 | 第4月 | 第5月 |
甲 | 6 | 9 | 10 | 8 | 8 |
乙 | 5 | 7 | 8 | 9 | 9 |
丙 | 5 | 9 | 10 | 5 | 11 |
(1)根据上表中的数据,将下表补充完整:
统计值 数值 人员 | 平均数(万元) | 众数(万元) | 中位数(万元) | 方差 |
甲 | 8 | 8 | 1.76 | |
乙 | 7.6 | 8 | 2.24 | |
丙 | 8 | 5 |
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.
科目:初中数学 来源: 题型:
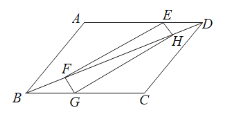
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD ,BC上,顶点F,H在菱形ABCD的对角线BD上,若AB=6,∠A=120°,且DE=2,则FH=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
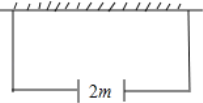
【题目】如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,墙对面有一个2m宽的门,另三边用竹篱笆围成,篱笆总长33m.围成长方形的养鸡场除门之外四周不能有空隙.
(1)若墙长为18m,要围成养鸡场的面积为150m2,则养鸡场的长和宽各为多少?
(2)围成养鸡场的面积能否达到200m2?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小夏同学从家到学校有![]() ,
,![]() 两条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
两条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时 频数 公交车路线 |
|
|
|
| 总计 |
| 59 | 151 | 166 | 124 | 500 |
| 43 | 57 | 149 | 251 | 500 |
据此估计,早高峰期间,乘坐![]() 线路“用时不超过35分钟”的概率为__________,若要在40分钟之内到达学校,应尽量选择乘坐__________(填
线路“用时不超过35分钟”的概率为__________,若要在40分钟之内到达学校,应尽量选择乘坐__________(填![]() 或
或![]() )线路.
)线路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据北京市统计局发布的统计数据显示,北京市近五年国民生产总值数据如图1所示,2017年国民生产总值中第一产业、第二产业、第三产业所占比例如图2所示,根据以上信息,下列判断错误的是( )
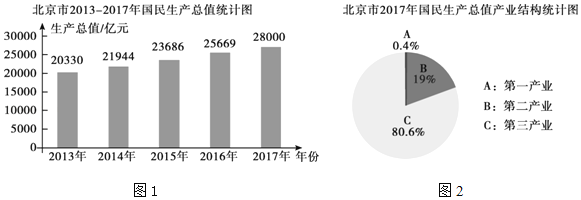
A.2013年至2017年北京市国民生产总值逐年增加
B.2017年第二产业生产总值为5 320亿元
C.2017年比2016年的国民生产总值增加了10%
D.若从2018年开始,每一年的国民生产总值比前一年均增长10%,到2019年的国民生产总值将达到33 880亿元
查看答案和解析>>
科目:初中数学 来源: 题型:
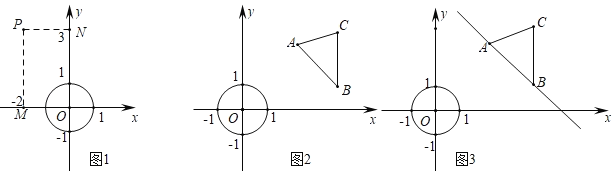
【题目】在平面直角坐标系xOy,对于点P(xp,yp)和图形G,设Q(xQ,yQ)是图形G上任意一点,|xp﹣xQ|的最小值叫点P和图形G的“水平距离”,|yp﹣yQ|的最小值叫点P和图形G的“竖直距离”,点P和图形G的“水平距离”与“竖直距离”的最大值叫做点P和图形G的“绝对距离”
例如:点P(﹣2,3)和半径为1的⊙O,因为⊙O上任一点Q(xQ,yQ)满足﹣1≤xQ≤1,﹣1≤yQ≤1,点P和⊙O的“水平距离”为|﹣2﹣xQ|的最小值,即|﹣2﹣(﹣1)|=1,点P和⊙O的“竖直距离”为|3﹣yQ|的最小值即|3﹣1|=2,因为2>1,所以点P和⊙O的“绝对距离”为2.
已知⊙O半径为1,A(2,![]() ),B(4,1),C(4,3)
),B(4,1),C(4,3)
(1)①直接写出点A和⊙O的“绝对距离”
②已知D是△ABC边上一个动点,当点D与⊙O的“绝对距离”为2时,写出一个满足条件的点D的坐标;
(2)已知E是△ABC边一个动点,直接写出点E与⊙O的“绝对距离”的最小值及相应的点E的坐标
(3)已知P是⊙O上一个动点,△ABC沿直线AB平移过程中,直接写出点P与△ABC的“绝对距离”的最小值及相应的点P和点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备开办“书画、器乐、戏曲、棋类”四个兴趣班.为了解学生对兴趣班的选择情况,随机抽取部分学生调查.每人单选一项,结果如下(尚未完善).
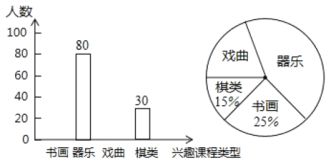
![]() 求本次调查的学生人数和扇形图中“器乐”对应圆心角的大小.
求本次调查的学生人数和扇形图中“器乐”对应圆心角的大小.
![]() 若全校共有
若全校共有![]() 名学生,请估计选择“戏曲”的人数.
名学生,请估计选择“戏曲”的人数.
![]() 学校将从四个兴趣班中任选取两个参加全区青少年才艺展示活动,求恰好抽到“器乐”和“戏曲”的概率.
学校将从四个兴趣班中任选取两个参加全区青少年才艺展示活动,求恰好抽到“器乐”和“戏曲”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数![]() ,一次函数
,一次函数![]() ,若方程
,若方程![]() 的两根是
的两根是![]() ,
,![]() .
.
(1)求b、c的值;
(2)当x满足![]() 时,比较
时,比较![]() 与x的大小并说明理由;
与x的大小并说明理由;
(3)设点M的坐标是![]() ,点P是抛物线
,点P是抛物线![]() 上的一个动点,当点P到点M的距离与到直线
上的一个动点,当点P到点M的距离与到直线![]() 的距离之和最小时,请直接写出点P坐标.
的距离之和最小时,请直接写出点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),C(0,3),点P是直线BC上方抛物线上的一动点,PE∥y轴,交直线BC于点E连接AP,交直线BC于点 D.
(1)求抛物线的函数表达式;
(2)当AD=2PD时,求点P的坐标;
(3)求线段PE的最大值;
(4)当线段PE最大时,若点F在直线BC上且∠EFP=2∠ACO,直接写出点F的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com