
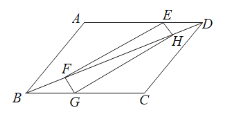
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD ,BC上,顶点F,H在菱形ABCD的对角线BD上,若AB=6,∠A=120°,且DE=2,则FH=_______.
【答案】![]()
【解析】
根据菱形的性质得到AD∥BC,得到∠GBF=∠EDH,可证明△BGF≌△DEH(AAS),得到BG=DE;连接GE,过点G作GQ//AB,交AD于点P,过点E作EQ⊥GQ,垂足为Q,证明四边形ABGP为平行四边形,得到AP=BG=2,∠GPE=120°,求得PE=2,∠EPQ=60°,进而求得PQ=1,QE=![]() ,运用勾股定理求得GE的长,从而可得FH的长.
,运用勾股定理求得GE的长,从而可得FH的长.
∵四边形EFGH是矩形,
∴EH=FG,EH∥FG,
∴∠GFH=∠EHF,
∵∠BFG=180°-∠GFH,∠DHE=180°-∠EHF,
∴∠BFG=∠DHE,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠GBF=∠EDH,
∴△BGF≌△DEH(AAS),
∴BG=DE;
∵DE=2,
∴BG=2;
过点G作GQ//AB,交AD于点P,过点E作EQ⊥GQ,垂足为Q,如图,
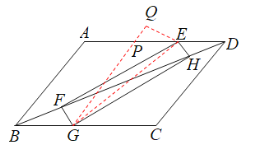
则四边形ABGP是平行四边形,
∴AP=BG=2,GP=AB=6,∠GPE=∠A=120°,
∴∠EPQ=60°,PE=AD-AP-DE=6-2-2=2
在Rt△PQE中 , ∠EPQ=60°,PE=2
∴∠QEP=30°,
∴QP=1
∴![]()
在Rt△GQE中,∠GQE=90°,GQ=GP+PQ=6+1=7,
∴![]()
∵四边形EFGH是矩形,
∴FH=GE=![]() .
.
故答案为:![]() .
.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】为弘扬祖国优秀传统文化,加强优秀文化熏陶,提高学生的文化素养和道德素质,我县某校举行了“经典启迪人生,国学伴我成长”主题活动,学校统一印制独具本校特色的国学教育校本教材,通过课堂教学和课外活动相结合的方式进行国学教育,为了解学生学习成果,现随机抽取了部分同学的国学成绩(x为整数,总分100分),绘制了如下尚不完整的统计图表.调查结果扇形统计图.
组别 | 成绩分组(单位:分) | 频数 | 频率 |
A | 50≤x<60 | 40 | 0.10 |
B | 60≤x<70 | 60 | c |
C | 70≤x<80 | a | 0.20 |
D | 80≤x<90 | 160 | 0.40 |
E | 90≤x<100 | 60 | 0.15 |
合计 | b | 1 |
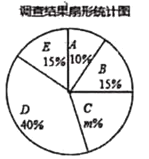
(1)根据以上信息解答问题:(1)统计表中a=________,b= ________,c=_______.
(2)扇形统计图中,m的值为________,“D”所对应的圆心角的度数是_______度;
(3)若参加国学教育的同学共有2000人,请你估计成绩在90分及以上的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() (
(![]() 左
左![]() 右),与
右),与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
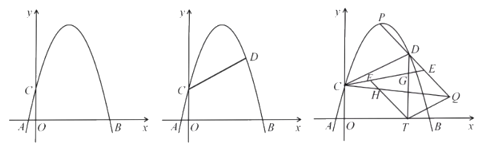
(1)求抛物线的解析式;
(2)如图2,点![]() 在第一象限抛物线上,连接
在第一象限抛物线上,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,如图3,过点![]() 作
作![]() 轴,线段
轴,线段![]() 经过点
经过点![]() ,与抛物线交于点
,与抛物线交于点![]() ,连接
,连接![]() 、
、![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
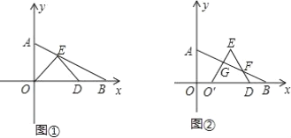
【题目】如图,在Rt△AOB中,∠ABO=30°,BO=4,分别以OA、OB边所在的直线建立平面直角坐标系,D点为x轴正半轴上的一点,以OD为一边在第一象限内作等边△ODE.
(1)如图①当E点恰好落在线段AB上时,求E点坐标;
(2)若点D从原点出发沿x轴正方向移动,设点D到原点的距离为x,△ODE与△AOB重叠部分的面积为y,当E点到达△AOB的外面,且点D在点B左侧时,写出y与x的函数关系式,并写出自变量x的取值范围;
(3)在(1)问的条件下,将△ODE在线段OB上向右平移如图②,图中是否存在一条与线段OO′始终相等的线段?如果存在,请直接指出这条线段;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
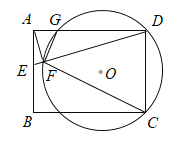
【题目】如图,在矩形ABCD中,E 是AB 上的一点,连接DE,过点A作AF⊥DE,垂直为F.圆O经过点C ,D ,F,且与AD相交于点G.
(1)求证,△AFG∽△DFC;
(2)若AB=3,BC=5,AE=1,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个三角形一条边上的高与这条边的比值是3:5,那么称这个三角形为“准黄金”三角形,这条边就叫做这个三角形的“金底”.
(概念感知)
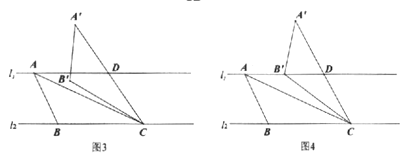
(1)如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,试判断
,试判断![]() 是否是“准黄金”三角形,请说明理由.
是否是“准黄金”三角形,请说明理由.

(问题探究)
(2)如图2,![]() 是“准黄金”三角形,BC是“金底”,把
是“准黄金”三角形,BC是“金底”,把![]() 沿BC翻折得到
沿BC翻折得到![]() ,连AB接AD交BC的延长线于点E,若点C恰好是
,连AB接AD交BC的延长线于点E,若点C恰好是![]() 的重心,求
的重心,求![]() 的值.
的值.
(拓展提升)
(3)如图3,![]() ,且直线
,且直线![]() 与
与![]() 之间的距离为3,“准黄金”
之间的距离为3,“准黄金”![]() 的“金底”BC在直线
的“金底”BC在直线![]() 上,点A在直线
上,点A在直线![]() 上.
上.![]() ,若
,若![]() 是钝角,将
是钝角,将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到
得到![]() ,线段
,线段![]() 交
交![]() 于点D.
于点D.
①当![]() 时,则
时,则![]() _________;
_________;
②如图4,当点B落在直线![]() 上时,求
上时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校教务处为了解九年级学生“居家学习”的学习能力,随机抽取该年级部分学生,对他们的学习能力进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图(其中学习能力指数级别“1”级,代表学习能力很强;“2”级,代表学习能力较强;“3”级,代表学习能力一般;“4“级,代表学习能力较弱)请结合图中相关数据回答问题.
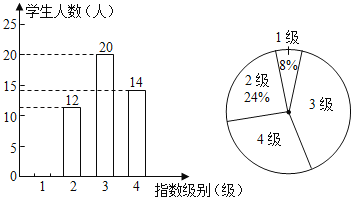
(1)本次抽查的学生人数 人,并将条形统计图补充完整;
(2)本次抽查学生“居家学习”能力指数级别的众数为 级,中位数为 级.
(3)已知学习能力很强的学生中只有1名女生,现从中随机抽取两人写有关“居家学习”的报告,请用列表或画树状图的方法求所抽查的两位学生中恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场甲、乙、丙三名业务员2018年前5个月的销售额(单位:万元)如下表:
月份 销售额 人员 | 第1月 | 第2月 | 第3月 | 第4月 | 第5月 |
甲 | 6 | 9 | 10 | 8 | 8 |
乙 | 5 | 7 | 8 | 9 | 9 |
丙 | 5 | 9 | 10 | 5 | 11 |
(1)根据上表中的数据,将下表补充完整:
统计值 数值 人员 | 平均数(万元) | 众数(万元) | 中位数(万元) | 方差 |
甲 | 8 | 8 | 1.76 | |
乙 | 7.6 | 8 | 2.24 | |
丙 | 8 | 5 |
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com