
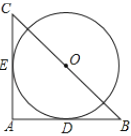
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,以BC的中点O为圆心的
,以BC的中点O为圆心的![]() 分别与AB,AC相切于D,E两点,则
分别与AB,AC相切于D,E两点,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.

(1)在旋转过程中,
①当A,D,M三点在同一直线上时,求AM的长.
②当A,D,M三点为同一直角三角形的顶点时,求AM的长.
(2)若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,连结D1D2,如图2,此时∠AD2C=135°,CD2=60,求BD2的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
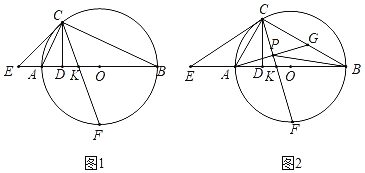
【题目】如图1,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D,E是BA廷长线上一点,连接CE,∠ACE=∠ACD,K是线段AO上一点,连接CK并延长交⊙O于点F.
(1)求证:CE是⊙O的切线;
(2)若AD=DK,求证:AKAO=KBAE;
(3)如图2,若AE=AK,![]() ,点G是BC的中点,AG与CF交于点P,连接BP.请猜想PA,PB,PF的数量关系,并证明.
,点G是BC的中点,AG与CF交于点P,连接BP.请猜想PA,PB,PF的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承优秀传统文化,某校团委组织了一次全校1000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了200名学生的成绩(成绩![]() 取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩 | 频数 | 频率 |
| 10 | 0.05 |
| 20 | 0.10 |
| 30 |
|
|
| 0.30 |
| 80 | 0.40 |
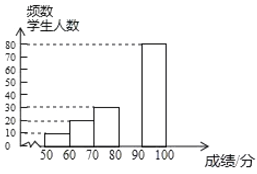
请根据所给的信息,解答下列问题:
(1)![]() _____,
_____,![]() _____;
_____;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在______分数段;
(4)若成绩在90分以上(包括90分)的为优等,则该校参加这次比赛的1000名学生中成绩优等的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
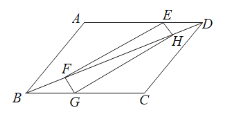
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD ,BC上,顶点F,H在菱形ABCD的对角线BD上,若AB=6,∠A=120°,且DE=2,则FH=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
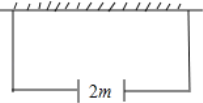
【题目】如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,墙对面有一个2m宽的门,另三边用竹篱笆围成,篱笆总长33m.围成长方形的养鸡场除门之外四周不能有空隙.
(1)若墙长为18m,要围成养鸡场的面积为150m2,则养鸡场的长和宽各为多少?
(2)围成养鸡场的面积能否达到200m2?请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com