
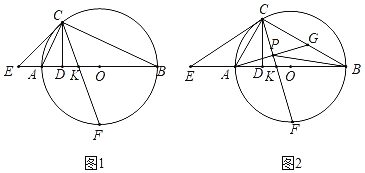
【题目】如图1,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D,E是BA廷长线上一点,连接CE,∠ACE=∠ACD,K是线段AO上一点,连接CK并延长交⊙O于点F.
(1)求证:CE是⊙O的切线;
(2)若AD=DK,求证:AKAO=KBAE;
(3)如图2,若AE=AK,![]() ,点G是BC的中点,AG与CF交于点P,连接BP.请猜想PA,PB,PF的数量关系,并证明.
,点G是BC的中点,AG与CF交于点P,连接BP.请猜想PA,PB,PF的数量关系,并证明.
【答案】(1)详见解析;(2)详见解析;(3)PA2+PF2=PB2,证明详见解析.
【解析】
(1)连接OC,先由证明∠CAD=∠ACO,再由∠ACE=∠ACD,可证得∠ECO=90°,即可证明;
(2)先证得∠ACE=∠B,∠CAE=∠BKC,说明△CAE∽△BKC,利用相似三角形的性质推得ACKC=AEKB,再由∠CAD=∠CKD,∠CAD=∠OCA,判定△OCA∽△CAK,利用相似三角形的性质推得ACKC=AKAO,从而可得结论;
(3)结论:PA2+PF2=PB2.连接AF、BF,先证得∠ACE=∠CBE,∠E=∠E,从而△EAC∽△ECB,由相似三角形的性质推得BC=2AC,再设AC=CG=GB=x,则AG=![]() ,从而
,从而![]() ,结合∠PGB=∠BGA,可得△PGB∽△BGA,进而推得BP=BF=AF,然后运用勾股定理证即可得到结论.
,结合∠PGB=∠BGA,可得△PGB∽△BGA,进而推得BP=BF=AF,然后运用勾股定理证即可得到结论.
解:(1)证明:连接OC,如图所示:
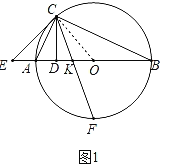
∵CD⊥AB,
∴∠CAD+∠ACD=90°,
∵OA=OC,
∴∠CAD=∠ACO,
又∵∠ACE=∠ACD,
∴∠ACE+∠ACO=90°,即∠ECO=90°,
∴CE是⊙O的切线;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAD+∠B=90°,
又∵∠CAD+∠ACD=90°,∠ACD=∠B,
∴∠ACE=∠B,
∵AD=DK,CD⊥AB,
∴CA=CK,∠CAD=∠CKD,
∴∠CAE=∠BKC,
∴△CAE∽△BKC,
∴![]() ,
,
∴ACKC=AEKB,
又∵∠CAD=∠CKD,∠CAD=∠OCA,
∴△OCA∽△CAK,
∴![]()
∴ACKC=AKAO,
∴AKAO=KBAE;
(3)PA2+PF2=PB2.理由如下:
如图,连接AF、BF,
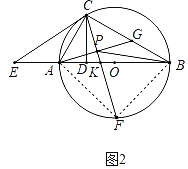
∵![]() ,
,
∴∠ACF=∠BCF=![]() ∠ACB=45°,AF=BF,
∠ACB=45°,AF=BF,
∴∠ECK=∠ACK+∠ACE=45°+∠ACE,∠EKC=∠BCK+∠KBC=45°+∠ABC,
∴∠ECK=∠EKC,
∴EC=EK=AE+EK=2AE,
∵∠ACE=∠CBE,∠E=∠E,
∴△EAC∽△ECB,
∴![]() ,
,
∴BC=2AC,
∵点G是BC的中点,
∴BC=2CG=2GB,
∴AC=CG,∠ACF=∠BCF,
∴CP⊥AG,AP=PG,
设AC=CG=GB=x,
则AG=![]() ,
,
∴![]() ,
,
又∠PGB=∠BGA,
∴△PGB∽△BGA,
∴∠GBP=∠GAB,
∴∠GBP+∠BCF=∠GAB+∠GAC,
即∠BPF=∠BAC=∠BFP,
∴BP=BF=AF,
∵在Rt△APF中,PA2+PF2=AF2,
∴PA2+PF2=PB2.


科目:初中数学 来源: 题型:
【题目】![]() ,
,![]() 两地相距
两地相距![]() ,甲、乙两人都由
,甲、乙两人都由![]() 地去
地去![]() 地,甲骑自行车,平均速度为
地,甲骑自行车,平均速度为![]() ;乙乘汽车,平均速度为
;乙乘汽车,平均速度为![]() ,且比甲晚
,且比甲晚![]() 出发.设甲的骑行时间为
出发.设甲的骑行时间为![]()
![]() .
.
(1)根据题意,填写表格:
时间 与 | 0.5 | 1.8 | |
甲与 | 5 | 20 | |
乙与 | 0 | 12 |
(2)设甲,乙两人与![]() 地的距离为
地的距离为![]() 和
和![]() .写出
.写出![]() ,
,![]() 关于
关于![]() 的表达式;
的表达式;
(3)设甲,乙两人之间的距离为![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬祖国优秀传统文化,加强优秀文化熏陶,提高学生的文化素养和道德素质,我县某校举行了“经典启迪人生,国学伴我成长”主题活动,学校统一印制独具本校特色的国学教育校本教材,通过课堂教学和课外活动相结合的方式进行国学教育,为了解学生学习成果,现随机抽取了部分同学的国学成绩(x为整数,总分100分),绘制了如下尚不完整的统计图表.调查结果扇形统计图.
组别 | 成绩分组(单位:分) | 频数 | 频率 |
A | 50≤x<60 | 40 | 0.10 |
B | 60≤x<70 | 60 | c |
C | 70≤x<80 | a | 0.20 |
D | 80≤x<90 | 160 | 0.40 |
E | 90≤x<100 | 60 | 0.15 |
合计 | b | 1 |
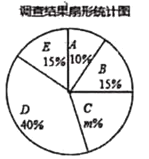
(1)根据以上信息解答问题:(1)统计表中a=________,b= ________,c=_______.
(2)扇形统计图中,m的值为________,“D”所对应的圆心角的度数是_______度;
(3)若参加国学教育的同学共有2000人,请你估计成绩在90分及以上的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
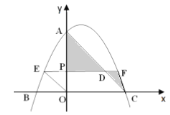
【题目】如图,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,点
两点,点![]() 是线段
是线段![]() 上的一个动点,过
上的一个动点,过![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() (点
(点![]() 在点
在点![]() 的左侧).
的左侧).
(1)求抛物线的解析式.
(2)当四边形![]() 是平行四边形时,求点
是平行四边形时,求点![]() 的坐标.
的坐标.
(3)设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1)、(2)题.
数学课上,老师出示了这样一道题:![]() 中,
中,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() 垂足为
垂足为![]() ,探究线段
,探究线段![]() 与
与![]() 的数量关系,并证明.
的数量关系,并证明.
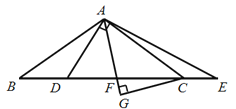
同学们经过思考后,交流了自己的想法:
小明:“通过观察和度量,发现![]() 与
与![]() 相等.”
相等.”
小强:“通过观察和度量,发现图中还有其它相等线段.”
小伟:“通过构造全等三角形,经过进一步推理,可以得到线段![]() 与
与![]() 的数量关系.”
的数量关系.”
……
老师:“此题还有其它解法,同学们课后可以继续探究,互相交流.”
……
(1)求证:![]() ;
;
(2)探究线段![]() 与
与![]() 的数量关系(用含
的数量关系(用含![]() 的代数式表示),并证明.
的代数式表示),并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
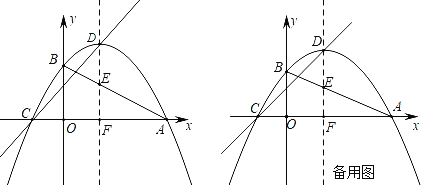
【题目】如图,抛物线y=ax2+x+c与x轴交于点A(6,0),C(﹣2,0),与y轴交于点B,抛物线的顶点为D,对称轴交AB于点E,交x轴于点F.
(1)求抛物线的解析式;
(2)P是抛物线上对称轴左侧一点,连接EP,若tan∠BEP=![]() ,求点P的坐标;
,求点P的坐标;
(3)M是直线CD上一点,N是抛物线上一点,试判断是否存在这样的点N,使得以点B,E,M,N为顶点的四边形是平行四边形,若存在,请直接写出点N的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() (
(![]() 左
左![]() 右),与
右),与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
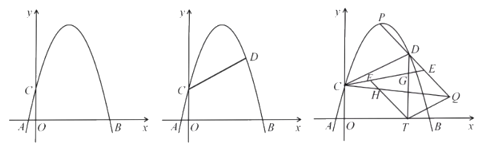
(1)求抛物线的解析式;
(2)如图2,点![]() 在第一象限抛物线上,连接
在第一象限抛物线上,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,如图3,过点![]() 作
作![]() 轴,线段
轴,线段![]() 经过点
经过点![]() ,与抛物线交于点
,与抛物线交于点![]() ,连接
,连接![]() 、
、![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校教务处为了解九年级学生“居家学习”的学习能力,随机抽取该年级部分学生,对他们的学习能力进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图(其中学习能力指数级别“1”级,代表学习能力很强;“2”级,代表学习能力较强;“3”级,代表学习能力一般;“4“级,代表学习能力较弱)请结合图中相关数据回答问题.
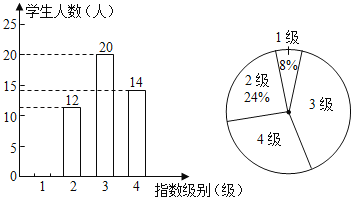
(1)本次抽查的学生人数 人,并将条形统计图补充完整;
(2)本次抽查学生“居家学习”能力指数级别的众数为 级,中位数为 级.
(3)已知学习能力很强的学生中只有1名女生,现从中随机抽取两人写有关“居家学习”的报告,请用列表或画树状图的方法求所抽查的两位学生中恰好是一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com