
����Ŀ���Ķ�������ϣ���ɣ�1������2���⣮
��ѧ���ϣ���ʦ��ʾ������һ���⣺![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ���ӳ����ϣ���
���ӳ����ϣ���![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ����Ϊ
����Ϊ![]() ��̽���߶�
��̽���߶�![]() ��
��![]() ��������ϵ����֤����
��������ϵ����֤����
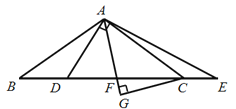
ͬѧ�Ǿ���˼���������Լ����뷨��
С������ͨ���۲�Ͷ���������![]() ��
��![]() ��ȣ���
��ȣ���
Сǿ����ͨ���۲�Ͷ���������ͼ�л�����������߶Σ���
Сΰ����ͨ������ȫ�������Σ�������һ�����������Եõ��߶�![]() ��
��![]() ��������ϵ����
��������ϵ����
����
��ʦ��������������ⷨ��ͬѧ�ǿκ���Լ���̽�������ཻ������
����
��1����֤��![]() ��
��
��2��̽���߶�![]() ��
��![]() ��������ϵ���ú�
��������ϵ���ú�![]() �Ĵ���ʽ��ʾ������֤����
�Ĵ���ʽ��ʾ������֤����
���𰸡���1�������� ��2��![]() �����ɼ�����
�����ɼ�����
��������
��1���ȸ��ݵ��������ε����ʵó�![]() ��Ȼ������
��Ȼ������![]() ��
��![]() �͵�����������֤�����ۣ�
�͵�����������֤�����ۣ�
��2������![]() ��
��![]() ����Ϊ
����Ϊ![]() ������
������![]() ��
��![]() ����Ϊ
����Ϊ![]() �������ý�ƽ���ߵĶ���͵��������εĶ��弰�������ڽǺͶ����ó�
�������ý�ƽ���ߵĶ���͵��������εĶ��弰�������ڽǺͶ����ó�![]() ����
����![]() ����ͨ�����������ó�
����ͨ�����������ó�![]() ����
����![]() ��������
��������![]() ��Ȼ��֤��
��Ȼ��֤��![]() ������
������![]() ����֤��
����֤��![]() ����
����![]() ����
����![]() ���Ӷ��ɵó�
���Ӷ��ɵó�![]() ��
��
��1��֤����![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
��2��![]() ���������£�
���������£�
��ͼ������![]() ��
��![]() ����Ϊ
����Ϊ![]() ������
������![]() ��
��![]() ����Ϊ
����Ϊ![]() ��
��
��![]() ��
��
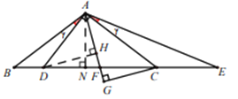
![]() ��
��
![]() ��
��
��![]() ����
����![]() ��
��
![]() ƽ��
ƽ��![]() ��
��
![]() ��
��
�ɣ�1��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]()
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��![]() ��
��![]() ��
�У�
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
 ��
��
![]() ��
��
![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
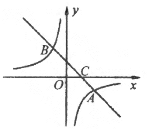
����Ŀ����ͼ��������y=ax2+bx+2��x����A����1��0����B��4��0�����㣬��y���ڵ�C�������C��ƽ����x���ֱ�߽�����һ��D����P����������һ���㣮
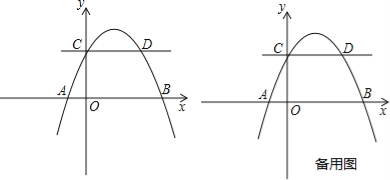
��1���������߽���ʽ����D���ꣻ
��2����E��x���ϣ�����A��E��D��PΪ������ı�����ƽ���ı��Σ����ʱ��P�����ꣻ
��3������P��ֱ��CD�Ĵ��ߣ�����ΪQ��������CPQ��CP���ۣ���Q�Ķ�Ӧ��ΪQ�����Ƿ���ڵ�P��ʹQ��ǡ������x���ϣ������ڣ������ʱ��P�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �IJ���ͼ����ͼ��ʾ����x���һ����������Ϊ
�IJ���ͼ����ͼ��ʾ����x���һ����������Ϊ![]() �������ߵĶԳ�����
�������ߵĶԳ�����![]() ���н����У�
�������
![]() ��
��![]() ��
��![]() ����
����![]() ����������ȵ�ʵ������
����������ȵ�ʵ������![]() ��������x�����һ����������Ϊ
��������x�����һ����������Ϊ![]() ��
��![]() ����
����![]() �ڸ��������ϣ���
�ڸ��������ϣ���![]() ��
��
������ȷ����![]() ����
����![]()

A. 5�� B. 4�� C. 3�� D. 2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ���̴������г���8000Ԫ�����˴�ӣ�Һ�Сӣ�Ҹ�200ǧ�ˣ���ӣ�ҵĽ��۱�Сӣ�ҵĽ���ÿǧ�˶�20Ԫ.��ӣ���ۼ�Ϊÿǧ��40Ԫ��Сӣ���ۼ�Ϊÿǧ��16Ԫ.
(1)��ӣ�Һ�Сӣ�ҵĽ��۷ֱ���ÿǧ�˶���Ԫ?�������ˮ���̹��˶���ԪǮ?
(2)��ˮ���̵ڶ�������8000ԪǮ�������г������˴�ӣ�Һ�Сӣ�Ҹ�200ǧ�ˣ����۲��䣬�������������Сӣ�������20%����Сӣ�ҵ��ۼ۲��䣬Ҫ���õڶ�����Ǯ�����ڵ�һ����Ǯ��90%����ӣ�ҵ��ۼ�����ӦΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽����꼶�������������ɼ�����������ѡȡ���꼶�����������в��ԣ������Ǹ��ݲ��Գɼ����Ƶ�ͳ��ͼ����һ���֣�
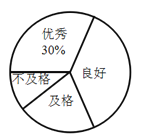
�ɼ��ȼ� | Ƶ�����ˣ� | Ƶ�� |
���� | ||
���� | ||
���� | 10 | 0��2 |
������ | 0��1 |
����������Ϣ������������⣺
��1�������������У��ɼ��ȼ�Ϊ�����㡱����������ռ�����������������İٷֱ�Ϊ________%���ɼ��ȼ�Ϊ��������������Ϊ________�ˣ�
��2��������������������Ϊ________�ˣ��ɼ��ȼ�Ϊ����������������________�ˣ�
��3������У���꼶����570�����������ݵ����������Ƹ�У���꼶�����ɼ��ȼ�Ϊ�����á���ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
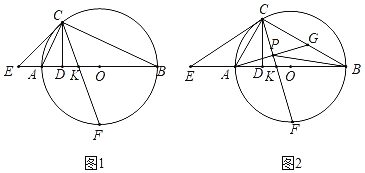
����Ŀ����ͼ1��AB����O��ֱ����C����O��һ�㣬CD��AB��D��E��BA͢������һ�㣬����CE����ACE����ACD��K���߶�AO��һ�㣬����CK���ӳ�����O�ڵ�F��
��1����֤��CE����O�����ߣ�
��2����AD��DK����֤��AKAO��KBAE��
��3����ͼ2����AE��AK��![]() ����G��BC���е㣬AG��CF���ڵ�P������BP�������PA��PB��PF��������ϵ����֤����
����G��BC���е㣬AG��CF���ڵ�P������BP�������PA��PB��PF��������ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
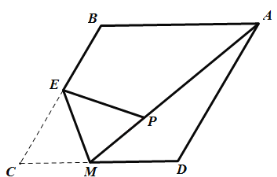
����Ŀ����ͼ��������![]() �У���
����![]() ��
��![]() �����е㣬����
�����е㣬����![]() ��
��![]() �����˶�����
�����˶�����![]() Ϊ�ۺ۽�
Ϊ�ۺ۽�![]() ���۵��õ�
���۵��õ�![]() ������
������![]() ����
����![]() ����
����![]() ����Сֵ��_____
����Сֵ��_____
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ı���![]() �У�
��![]() ����
����![]() ��ƽ���ı���
��ƽ���ı���![]() �ı��ϣ���
�ı��ϣ���![]() ������
������![]() ����
����![]() ��
��![]() �����߶�
�����߶�![]() �ij�Ϊ__________��
�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ����
��ͼ����![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() .
.
(1)��![]() ��ֵ;
��ֵ;
(2)��ֱ��д������ʽ![]() �Ľ⼯;
�Ľ⼯;
(3)��![]() ���·���ͼ����
���·���ͼ����![]() �ᷭ�ۣ���
�ᷭ�ۣ���![]() ���ڵ�
���ڵ�![]() ��������
��������![]() ����
����![]() �����.
�����.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com