
°Њћвƒњ°њ»зЌЉ£ђ≈„ќпѕяy=ax2+bx+2љїx÷б”ЏA£®©Б1£ђ0£©£ђB£®4£ђ0£©Ѕљµг£ђљїy÷б”ЏµгC£ђ”лєэµгC«“∆љ––”Џx÷бµƒ÷±ѕяљї”ЏЅн“їµгD£ђµгP «≈„ќпѕя…ѕ“їґѓµг£Ѓ
£®1£©«у≈„ќпѕяљвќц љЉ∞µгD„ш±к£ї
£®2£©µгE‘Џx÷б…ѕ£ђ»ф“‘A£ђE£ђD£ђPќ™ґ•µгµƒЋƒ±я–ќ «∆љ––Ћƒ±я–ќ£ђ«уіЋ ±µгPµƒ„ш±к£ї
£®3£©єэµгP„ч÷±ѕяCDµƒієѕя£ђіє„гќ™Q£ђ»фљЂ°чCPQ—ЎCPЈ≠’џ£ђµгQµƒґ‘”¶µгќ™Q°д£Ѓ «Јсіж‘ЏµгP£ђ єQ°д«°Ї√¬д‘Џx÷б…ѕ£њ»фіж‘Џ£ђ«у≥ціЋ ±µгPµƒ„ш±к£ї»ф≤їіж‘Џ£ђЋµ√чјн”…£Ѓ
°Њір∞Є°њ£®1£©![]() £ђµгD„ш±кќ™£®3£ђ2£©£®2£©P1£®0£ђ2£©£їP2£®
£ђµгD„ш±кќ™£®3£ђ2£©£®2£©P1£®0£ђ2£©£їP2£®![]() £ђ©Б2£©£їP3£®
£ђ©Б2£©£їP3£®![]() £ђ©Б2£©£®3£©іж‘Џ£ђ£®
£ђ©Б2£©£®3£©іж‘Џ£ђ£®![]() £©£ђ£®
£©£ђ£®![]() £©
£©
°Њљвќц°њ
љв£Ї£®1£©°я≈„ќпѕяy=ax2+bx+2Њ≠єэA£®©Б1£ђ0£©£ђB£®4£ђ0£©Ѕљµг£ђ
°а![]() £ђљвµ√£Ї
£ђљвµ√£Ї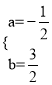 £Ѓ
£Ѓ
°а≈„ќпѕяљвќц љќ™![]() £Ѓ
£Ѓ
µ±y=2 ±£ђ![]() £ђљвµ√£Їx1=3£ђx2=0£®…б»•£©£Ѓ
£ђљвµ√£Їx1=3£ђx2=0£®…б»•£©£Ѓ
°аµгD„ш±кќ™£®3£ђ2£©£Ѓ
£®2£©A£ђEЅљµгґЉ‘Џx÷б…ѕ£ђAE”–Ѕљ÷÷њ…ƒ№£Ї
Ґўµ±AEќ™“ї±я ±£ђAE°ќPD£ђ°аP1£®0£ђ2£©£Ѓ
ҐЏµ±AEќ™ґ‘љ«ѕя ±£ђЄщЊЁ∆љ––Ћƒ±я–ќґ‘ґ•µгµљЅн“їћхґ‘љ«ѕяЊајлѕаµ»£ђњ…÷™Pµг°ҐDµгµљ÷±ѕяAE£®Љіx÷б£©µƒЊајлѕаµ»£ђ°аPµгµƒ„Ё„ш±кќ™©Б2£Ѓ
іъ»л≈„ќпѕяµƒљвќц љ£Ї![]() £ђљвµ√£Ї
£ђљвµ√£Ї![]() £Ѓ
£Ѓ
°аPµгµƒ„ш±кќ™£®![]() £ђ©Б2£©£ђ£®
£ђ©Б2£©£ђ£®![]() £ђ©Б2£©£Ѓ
£ђ©Б2£©£Ѓ
„џ…ѕЋщ ц£ЇP1£®0£ђ2£©£їP2£®![]() £ђ©Б2£©£їP3£®
£ђ©Б2£©£їP3£®![]() £ђ©Б2£©£Ѓ
£ђ©Б2£©£Ѓ
£®3£©іж‘Џ¬ъ„гћхЉюµƒµгP£ђѕ‘»їµгP‘Џ÷±ѕяCDѕ¬Јљ£Ѓ
…и÷±ѕяPQљїx÷б”ЏF£ђµгPµƒ„ш±кќ™£®![]() £©£ђ
£©£ђ
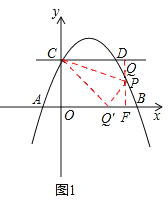
Ґўµ±Pµг‘Џy÷б”“≤а ±£®»зЌЉ1£©£ђCQ=a£ђ
PQ=![]() £Ѓ
£Ѓ
”÷°я°ѕCQ°дO+°ѕFQ°дP=90°г£ђ°ѕCOQ°д=°ѕQ°дFP=90°г£ђ
°а°ѕFQ°дP=°ѕOCQ°д£ђ°а°чCOQ°д°„°чQ°дFP£ђ
°а![]() £ђЉі
£ђЉі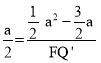 £ђљвµ√F Q°д=a©Б3
£ђљвµ√F Q°д=a©Б3
°аOQ°д=OF©БF Q°д=a©Б£®a©Б3£©=3£ђ
![]() £Ѓ
£Ѓ
іЋ ±a=![]() £ђµгPµƒ„ш±кќ™£®
£ђµгPµƒ„ш±кќ™£®![]() £©£Ѓ
£©£Ѓ
ҐЏµ±Pµг‘Џy÷б„у≤а ±£®»зЌЉ2£©іЋ ±a£Љ0£ђ£ђ![]() £Љ0£ђCQ=©Бa£ђ£®ќёЌЉ£©
£Љ0£ђCQ=©Бa£ђ£®ќёЌЉ£©
PQ=![]() £Ѓ
£Ѓ
”÷°я°ѕCQ°дO+°ѕFQ°дP=90°г£ђ°ѕCQ°дO+°ѕOCQ°д=90°г£ђ
°а°ѕFQ°дP=°ѕOCQ°д£ђ°ѕCOQ°д=°ѕQ°дFP=90°г£Ѓ
°а°чCOQ°д°„°чQ°дFP£Ѓ
°а![]() £ђЉі
£ђЉі £ђљвµ√F Q°д=3©Бa£Ѓ
£ђљвµ√F Q°д=3©Бa£Ѓ
°аOQ°д=3£ђ![]() £Ѓ
£Ѓ
іЋ ±a=©Б![]() £ђµгPµƒ„ш±кќ™£®
£ђµгPµƒ„ш±кќ™£®![]() £©£Ѓ
£©£Ѓ
„џ…ѕЋщ ц£ђ¬ъ„гћхЉюµƒµгP„ш±кќ™£®![]() £©£ђ£®
£©£ђ£®![]() £©£Ѓ
£©£Ѓ
£®1£©”√іэґ®ѕµ эЈ®њ…µ√≥ц≈„ќпѕяµƒљвќц љ£ђЅоy=2њ…µ√≥цµгDµƒ„ш±к£Ѓ
£®2£©Ј÷Ѕљ÷÷«йњцљш––ћ÷¬џ£ђҐўµ±AEќ™“ї±я ±£ђAE°ќPD£ђҐЏµ±AEќ™ґ‘љ«ѕя ±£ђЄщЊЁ∆љ––Ћƒ±я–ќґ‘ґ•µгµљЅн“їћхґ‘љ«ѕяЊајлѕаµ»£ђ«уљвµгP„ш±к£Ѓ
£®3£©љбЇѕЌЉ–ќњ…≈–ґѕ≥цµгP‘Џ÷±ѕяCDѕ¬Јљ£ђ…иµгPµƒ„ш±кќ™£®![]() £©£ђЈ÷«йњцћ÷¬џ£ђҐўµ±Pµг‘Џy÷б”“≤а ±£ђҐЏµ±Pµг‘Џy÷б„у≤а ±£ђ‘Ћ”√љв÷±љ«»эљ«–ќЉ∞ѕаЋ∆»эљ«–ќµƒ–‘÷ љш––«уљвЉіњ…£Ѓ
£©£ђЈ÷«йњцћ÷¬џ£ђҐўµ±Pµг‘Џy÷б”“≤а ±£ђҐЏµ±Pµг‘Џy÷б„у≤а ±£ђ‘Ћ”√љв÷±љ«»эљ«–ќЉ∞ѕаЋ∆»эљ«–ќµƒ–‘÷ љш––«уљвЉіњ…£Ѓ


 –°—Іљћ≤ƒ»Ђ≤вѕµЅ–ір∞Є
–°—Іљћ≤ƒ»Ђ≤вѕµЅ–ір∞Є –°—І э—ІњЏЋгћвњ®Ќ—њЏґш≥цѕµЅ–ір∞Є
–°—І э—ІњЏЋгћвњ®Ќ—њЏґш≥цѕµЅ–ір∞Є ”≈–г…ъ”¶”√ћвњ®њЏЋгћмћмЅЈѕµЅ–ір∞Є
”≈–г…ъ”¶”√ћвњ®њЏЋгћмћмЅЈѕµЅ–ір∞Є ’гљ≠÷Ѓ–«њќ ±”≈їѓ„ч“µѕµЅ–ір∞Є
’гљ≠÷Ѓ–«њќ ±”≈їѓ„ч“µѕµЅ–ір∞Є
| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
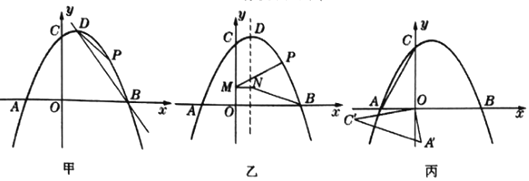
°Њћвƒњ°њ»зЌЉЉ„Ћщ Њ£ђ‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–£ђ≈„ќпѕя![]() ”л
”л![]() ÷бљї”Џ
÷бљї”Џ![]() £ђ
£ђ![]() Ѕљµг£ђ”л
Ѕљµг£ђ”л![]() ÷бљї”Џµг
÷бљї”Џµг![]() £ђµг
£ђµг![]() ќ™Є√≈„ќпѕяµƒґ•µг£Ѓ
ќ™Є√≈„ќпѕяµƒґ•µг£Ѓ
£®1£©»зЌЉЉ„£ђµг![]() ќ™≈„ќпѕя…ѕ
ќ™≈„ќпѕя…ѕ![]() £ђ
£ђ![]() ЅљµгЉдµƒ“їґѓµг£ђЅђљ”
ЅљµгЉдµƒ“їґѓµг£ђЅђљ”![]() £ђ
£ђ![]() £ђµ±
£ђµ±![]() √жїэ„оіу ±£ђ‘Џґ‘≥∆÷б…ѕ”–“їґѓµг
√жїэ„оіу ±£ђ‘Џґ‘≥∆÷б…ѕ”–“їґѓµг![]() £ђ»зЌЉ““Ћщ Њ£ђєэµг
£ђ»зЌЉ““Ћщ Њ£ђєэµг![]() „ч
„ч![]() ÷бљї
÷бљї![]() ÷б”Џµг
÷б”Џµг![]() £ђЅђљ”
£ђЅђљ”![]() £ђ
£ђ![]() £ђ«у
£ђ«у![]() µƒ„о–°÷µ£ђ≤Ґ«у≥ціЋ ±µг
µƒ„о–°÷µ£ђ≤Ґ«у≥ціЋ ±µг![]() µƒ„ш±к£ї
µƒ„ш±к£ї
£®2£©»зЌЉ±ыЋщ Њ£ђљЂ![]() »∆„≈µг
»∆„≈µг![]() –э„™£ђµ√µљ
–э„™£ђµ√µљ![]() £ђ‘Џ–э„™єэ≥ћ÷–£ђ «Јсіж‘Џƒ≥Єц ±њћ є“‘µг
£ђ‘Џ–э„™єэ≥ћ÷–£ђ «Јсіж‘Џƒ≥Єц ±њћ є“‘µг![]() ќ™ґ•µгµƒ»эљ«–ќќ™“‘
ќ™ґ•µгµƒ»эљ«–ќќ™“‘![]() ќ™—ьµƒµ»—ь»эљ«–ќ£ђ»зєыіж‘Џ£ђ«л÷±љ”–і≥ціЋ ±µг
ќ™—ьµƒµ»—ь»эљ«–ќ£ђ»зєыіж‘Џ£ђ«л÷±љ”–і≥ціЋ ±µг![]() µƒ„ш±к£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£Ѓ
µƒ„ш±к£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
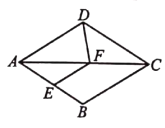
°Њћвƒњ°њ»зЌЉ£ђЅв–ќ![]() µƒ±я≥§ќ™
µƒ±я≥§ќ™![]() £ђµг
£ђµг![]() «±я
«±я![]() …ѕ“їґѓµг(≤ї”лµг
…ѕ“їґѓµг(≤ї”лµг![]() ÷ЎЇѕ)£ђєэµг
÷ЎЇѕ)£ђєэµг![]() „ч
„ч![]() љї
љї![]() ”Џµг
”Џµг![]() Ѕђљ”
Ѕђљ”![]() µ±
µ±![]() «µ»—ь»эљ«–ќ ±£ђ
«µ»—ь»эљ«–ќ ±£ђ![]() µƒ≥§µ»”Џ __________________£Ѓ
µƒ≥§µ»”Џ __________________£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
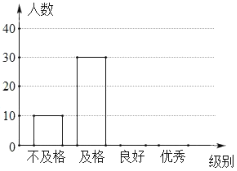
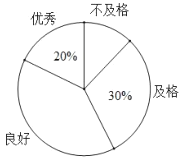
°Њћвƒњ°њ–¬єЏЈќ—„“я«йЈҐ…ъ“‘јі£ђ„®Љ“Єш≥цЅЋЇ№ґа‘§Јјљ®“й£Ѓќ™∆’Љ∞‘§Јјіл ©£ђƒ≥–£„й÷ѓЅЋ”…∞ЋƒкЉґ800√ы—І…ъ≤ќЉ”µƒ°∞Јј–¬єЏ°±÷™ ґЊЇ»ь£Ѓјојѕ ¶ќ™ЅЋЅЋљв—І…ъµƒірћв«йњц£ђі”÷–Ћжїъ≥й»°ЅЋ≤њЈ÷Ќђ—Іµƒ≥…Љ®„чќ™—щ±Њ£ђ∞—≥…Љ®∞і”≈–г°ҐЅЉЇ√°ҐЉ∞Єс°Ґ≤їЉ∞Єс4ЄцЉґ±рљш––Ќ≥Љ∆£ђ≤Ґїж÷∆≥…ЅЋ»зЌЉµƒћх–ќЌ≥Љ∆ЌЉЇЌ…»–ќЌ≥Љ∆ЌЉ£®≤њЈ÷–≈ѕҐќіЄш≥ц£©£Ѓ
«лЄщЊЁ“‘…ѕћбє©µƒ–≈ѕҐ£ђљвірѕ¬Ѕ–ќ ћв£Ї
£®1£©«у±ї≥й»°µƒ≤њЈ÷—І…ъµƒ»Ћ э£ї
£®2£©«л≤є»Ђћх–ќЌ≥Љ∆ЌЉ£ї
£®3£©«у≥ц…»–ќЌ≥Љ∆ЌЉ÷–±н ЊЅЉЇ√Љґ±рµƒ…»–ќµƒ‘≤–ƒљ«ґ» э£ї
£®4£©«лєјЉ∆∞ЋƒкЉґµƒ800√ы—І…ъ÷–іпµљЅЉЇ√ЇЌ”≈–гµƒ„№»Ћ э£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ‘Џ°чABC÷–£ђ°ѕBAC£љ90°г£ђµгO‘ЏBC…ѕ£ђ“‘ѕяґќOCµƒ≥§ќ™∞лЊґµƒ°—O”лABѕа«–”ЏµгD£ђЈ÷±рљїBC°ҐAC”ЏµгE°ҐF£ђЅђљ”ED≤Ґ—”≥§£ђљїCAµƒ—”≥§ѕя”ЏµгG£Ѓ
£®1£©«у÷§£Ї°ѕDOC£љ2°ѕG£Ѓ
£®2£©“—÷™°—Oµƒ∞лЊґќ™3£Ѓ
Ґў»фBE£љ2£ђ‘тDA£љ°° °°£Ѓ
ҐЏµ±BE£љ°° °° ±£ђЋƒ±я–ќDOCFќ™Ѕв–ќ£Ѓ

≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ![]() £ђ
£ђ![]() ЅљµЎѕаЊа
ЅљµЎѕаЊа![]() £ђЉ„°Ґ““Ѕљ»ЋґЉ”…
£ђЉ„°Ґ““Ѕљ»ЋґЉ”…![]() µЎ»•
µЎ»•![]() µЎ£ђЉ„∆п„‘––≥µ£ђ∆љЊщЋўґ»ќ™
µЎ£ђЉ„∆п„‘––≥µ£ђ∆љЊщЋўґ»ќ™![]() £ї““≥Ћ∆ы≥µ£ђ∆љЊщЋўґ»ќ™
£ї““≥Ћ∆ы≥µ£ђ∆љЊщЋўґ»ќ™![]() £ђ«“±»Љ„Ќн
£ђ«“±»Љ„Ќн![]() ≥цЈҐ.…иЉ„µƒ∆п–– ±Љдќ™
≥цЈҐ.…иЉ„µƒ∆п–– ±Љдќ™![]()
![]() £Ѓ
£Ѓ
£®1£©ЄщЊЁћв“в£ђћо–і±нЄс£Ї
±Љд ”л | 0.5 | 1.8 | |
Љ„”л | 5 | 20 | |
““”л | 0 | 12 |
£®2£©…иЉ„£ђ““Ѕљ»Ћ”л![]() µЎµƒЊајлќ™
µЎµƒЊајлќ™![]() ЇЌ
ЇЌ![]() .–і≥ц
.–і≥ц![]() £ђ
£ђ![]() єЎ”Џ
єЎ”Џ![]() µƒ±ніп љ£ї
µƒ±ніп љ£ї
£®3£©…иЉ„£ђ““Ѕљ»Ћ÷ЃЉдµƒЊајлќ™![]() £ђµ±
£ђµ±![]() ±£ђ«у
±£ђ«у![]() µƒ»°÷µЈґќІ.
µƒ»°÷µЈґќІ.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
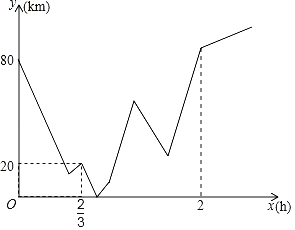
°Њћвƒњ°њA°ҐBЅљµЎ÷ЃЉд”–“ї–ёјн≥ІC£ђ“ї»’–°Ї£ЇЌЌх¬љЈ÷±рі”A°ҐBЅљµЎЌђ ±≥цЈҐѕаѕтґш––£ђЌх¬љњ™≥µ£ђ–°Ї£∆пƒ¶Ќ–£Ѓґю»Ћѕа”ц ±–°Ї£µƒƒ¶Ќ–≥µЌї»ї≥цє ’ѕќёЈ®«∞––£ђЌх¬љЊцґ®љЂ–°Ї£ЇЌƒ¶Ќ–≥µ“ї∆рЋЌїЎµљ–ёјн≥ІCЇу‘ўЉћ–ш∞і‘≠¬Ј«∞––£ђЌх¬љµљіпAµЎЇуЅҐЉіЈµїЎBµЎ£ђµљBµЎЇу≤ї‘ўЉћ–ш«∞––£ђµ»іэ–°Ї£«∞јі£®„∞‘Ўƒ¶Ќ–≥µ ±ЉдЇЌµфЌЈ ±ЉдЇц¬‘≤їЉ∆£©£ђ’ыЄц–– їєэ≥ћ÷–Ќх¬љЋўґ»≤ї±д£ђґш–°Ї£‘Џ–ёјн≥Ії®ЅЋ ЃЈ÷÷”–ёЇ√ƒ¶Ќ–≥µ£ђќ™ЅЋЄѕ ±Љд£ђћбЋў![]() «∞ЌщƒњµƒµЎB£ђ–°Ї£µљіпBµЎЇу“≤љб ш––≥ћ£ђ»фЌЉѕу±н Њµƒ «–°Ї£”лЌх¬љґю»Ћµљ–ёјн≥ІCµƒЊајлЇЌy£®km£©”л–°Ї£≥ц–– ±Љд÷ЃЉдx£®h£©µƒєЎѕµ£ђ‘тµ±Ќх¬љµЏґюіќ”л–°Ї£‘Џ–– ї÷–ѕа”ц ±£ђ–°Ї£јлƒњµƒµЎBїє”–_____km£Ѓ
«∞ЌщƒњµƒµЎB£ђ–°Ї£µљіпBµЎЇу“≤љб ш––≥ћ£ђ»фЌЉѕу±н Њµƒ «–°Ї£”лЌх¬љґю»Ћµљ–ёјн≥ІCµƒЊајлЇЌy£®km£©”л–°Ї£≥ц–– ±Љд÷ЃЉдx£®h£©µƒєЎѕµ£ђ‘тµ±Ќх¬љµЏґюіќ”л–°Ї£‘Џ–– ї÷–ѕа”ц ±£ђ–°Ї£јлƒњµƒµЎBїє”–_____km£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–£ђµг![]() ќ™„ш±к‘≠µг£ђ≈„ќпѕя
ќ™„ш±к‘≠µг£ђ≈„ќпѕя![]() ”л
”л![]() ÷бљї”Џµг
÷бљї”Џµг![]() £ђµг
£ђµг![]() £ђ”л
£ђ”л![]() ÷бљї”Џµг
÷бљї”Џµг![]() £ђЅђљ”
£ђЅђљ”![]() £ђµг
£ђµг![]() ‘ЏµЏґюѕуѕёµƒ≈„ќпѕя…ѕ£ђЅђљ”
‘ЏµЏґюѕуѕёµƒ≈„ќпѕя…ѕ£ђЅђљ”![]() £ђѕяґќ
£ђѕяґќ![]() љїѕяґќ
љїѕяґќ![]() ”Џµг
”Џµг![]() £Ѓ
£Ѓ
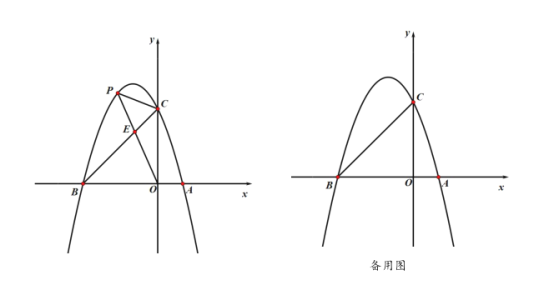
£®1£©«у≈„ќпѕяµƒ±ніп љ£ї
£®2£©»ф![]() µƒ√жїэќ™
µƒ√жїэќ™![]() £ђ
£ђ![]() µƒ√жїэќ™
µƒ√жїэќ™![]() µ±
µ±![]() ±£ђ«уµг
±£ђ«уµг![]() µƒ„ш±к£ї
µƒ„ш±к£ї
£®3£©“—÷™µг![]() єЎ”Џ≈„ќпѕяґ‘≥∆÷бµƒґ‘≥∆µгќ™µг
єЎ”Џ≈„ќпѕяґ‘≥∆÷бµƒґ‘≥∆µгќ™µг![]() £ђЅђљ”
£ђЅђљ”![]() £ђµг
£ђµг![]() ‘Џ
‘Џ![]() ÷б…ѕ£ђµ±
÷б…ѕ£ђµ±![]() ±£ђ
±£ђ
Ґў«у¬ъ„гћхЉюµƒЋщ”–µг![]() µƒ„ш±к£ї
µƒ„ш±к£ї
ҐЏµ±µг![]() ‘Џѕяґќ
‘Џѕяґќ![]() …ѕ ±£ђµг
…ѕ ±£ђµг![]() «ѕяґќ
«ѕяґќ![]() Ќв“їµг£ђ
Ќв“їµг£ђ![]() £ђЅђљ”
£ђЅђљ”![]() £ђљЂѕяґќ
£ђљЂѕяґќ![]() »∆„≈µг
»∆„≈µг![]() Ћ≥ ±’л–э„™
Ћ≥ ±’л–э„™![]() £ђµ√µљѕяґќ
£ђµ√µљѕяґќ![]() £ђЅђљ”
£ђЅђљ”![]() £ђ÷±љ”–і≥цѕяґќ
£ђ÷±љ”–і≥цѕяґќ![]() µƒ»°÷µЈґќІ£Ѓ
µƒ»°÷µЈґќІ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
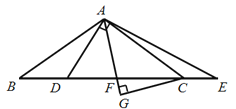
°Њћвƒњ°њ‘ƒґЅѕ¬√ж≤ƒЅѕ£ђЌк≥…£®1£©°Ґ£®2£©ћв£Ѓ
э—Іњќ…ѕ£ђјѕ ¶≥ц ЊЅЋ’в—щ“їµјћв£Ї![]() ÷–£ђ
÷–£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]() љї
љї![]() ”Џµг
”Џµг![]() £ђµг
£ђµг![]() ‘Џ
‘Џ![]() µƒ—”≥§ѕя…ѕ£ђ«“
µƒ—”≥§ѕя…ѕ£ђ«“![]() £ђ
£ђ![]() ∆љЈ÷
∆љЈ÷![]() љї
љї![]() ”Џµг
”Џµг![]() £ђ
£ђ![]() іє„гќ™
іє„гќ™![]() £ђћљЊњѕяґќ
£ђћљЊњѕяґќ![]() ”л
”л![]() µƒ эЅњєЎѕµ£ђ≤Ґ÷§√ч£Ѓ
µƒ эЅњєЎѕµ£ђ≤Ґ÷§√ч£Ѓ
Ќђ—І√«Њ≠єэЋЉњЉЇу£ђљїЅчЅЋ„‘ЉЇµƒѕлЈ®£Ї
–°√ч£Ї°∞Ќ®єэєџ≤мЇЌґ»Ѕњ£ђЈҐѕ÷![]() ”л
”л![]() ѕаµ»£Ѓ°±
ѕаµ»£Ѓ°±
–°«њ£Ї°∞Ќ®єэєџ≤мЇЌґ»Ѕњ£ђЈҐѕ÷ЌЉ÷–їє”–∆дЋьѕаµ»ѕяґќ£Ѓ°±
–°ќ∞£Ї°∞Ќ®єэєє‘м»Ђµ»»эљ«–ќ£ђЊ≠єэљш“ї≤љЌ∆јн£ђњ…“‘µ√µљѕяґќ![]() ”л
”л![]() µƒ эЅњєЎѕµ£Ѓ°±
µƒ эЅњєЎѕµ£Ѓ°±
°≠°≠
јѕ ¶£Ї°∞іЋћвїє”–∆дЋьљвЈ®£ђЌђ—І√«њќЇуњ…“‘Љћ–шћљЊњ£ђї•ѕаљїЅч£Ѓ°±
°≠°≠
£®1£©«у÷§£Ї![]() £ї
£ї
£®2£©ћљЊњѕяґќ![]() ”л
”л![]() µƒ эЅњєЎѕµ£®”√Їђ
µƒ эЅњєЎѕµ£®”√Їђ![]() µƒіъ э љ±н Њ£©£ђ≤Ґ÷§√ч£Ѓ
µƒіъ э љ±н Њ£©£ђ≤Ґ÷§√ч£Ѓ
≤йњіір∞ЄЇЌљвќц>>
єъЉ —І–£”≈—° - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com