
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕу![]() ЮЊзјБъдЕуЃЌХзЮяЯп
ЮЊзјБъдЕуЃЌХзЮяЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЕу
ЃЌЕу![]() дкЕкЖўЯѓЯоЕФХзЮяЯпЩЯЃЌСЌНг
дкЕкЖўЯѓЯоЕФХзЮяЯпЩЯЃЌСЌНг![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() НЛЯпЖЮ
НЛЯпЖЮ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
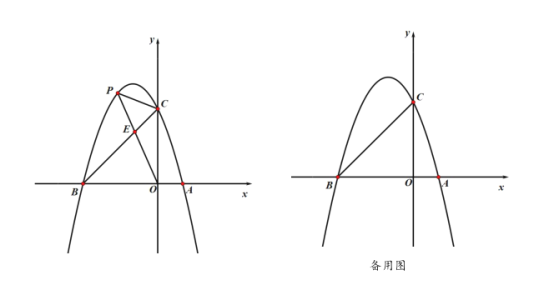
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉШє![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЕБ
ЕБ![]() ЪБЃЌЧѓЕу
ЪБЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉвбжЊЕу![]() ЙигкХзЮяЯпЖдГЦжсЕФЖдГЦЕуЮЊЕу
ЙигкХзЮяЯпЖдГЦжсЕФЖдГЦЕуЮЊЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() жсЩЯЃЌЕБ
жсЩЯЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ
ЂйЧѓТњзуЬѕМўЕФЫљгаЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЂкЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЪБЃЌЕу
ЩЯЪБЃЌЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЭтвЛЕуЃЌ
ЭтвЛЕуЃЌ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌНЋЯпЖЮ
ЃЌНЋЯпЖЮ![]() ШЦзХЕу
ШЦзХЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЃЌЕУЕНЯпЖЮ
ЃЌЕУЕНЯпЖЮ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌжБНгаДГіЯпЖЮ
ЃЌжБНгаДГіЯпЖЮ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() Лђ
Лђ![]() ЃЛЃЈ3ЃЉЂй
ЃЛЃЈ3ЃЉЂй![]() Лђ
Лђ![]() ЃЛЂк
ЃЛЂк![]()
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуAЁЂBзјБъДњШыНтЮіЪННтД№МДПЩЃЛ
ЃЈ2ЃЉЯШЧѓГіЕуCЕФзјБъЮЊЃЈ0,3ЃЉЃЌЙ§ЕуCзїCGЁЭOPгкGЃЌИљОн![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕУЕН
ЕУЕН![]() ЃЌЙ§ЕуPзїPFЁЭxжсгкFЃЌЙ§ЕуEзїENЁЭPFгкNЃЌЕУЕН
ЃЌЙ§ЕуPзїPFЁЭxжсгкFЃЌЙ§ЕуEзїENЁЭPFгкNЃЌЕУЕН![]() ЃЌЩшЕуPЕФзјБъЮЊЃЈaЃЌ
ЃЌЩшЕуPЕФзјБъЮЊЃЈaЃЌ![]() ЃЉЃЌЧѓГіжБЯпBCЕФНтЮіЪНЮЊy=x+3ЃЌЕУЕНEЃЈ
ЃЉЃЌЧѓГіжБЯпBCЕФНтЮіЪНЮЊy=x+3ЃЌЕУЕНEЃЈ![]() ЃЌ
ЃЌ![]() +3ЃЉЃЌИљОн2PF=5PNЕУЕН5(
+3ЃЉЃЌИљОн2PF=5PNЕУЕН5(![]() -
-![]() -3)=2(
-3)=2(![]() )ЃЌЧѓГіxжЕМДПЩЕУЕНЕуPЕФзјБъЃЛ
)ЃЌЧѓГіxжЕМДПЩЕУЕНЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЂйЯШЧѓГіХзЮяЯпЕФЖдГЦжсЪЧжБЯпx=-1ЃЌЕУЕНNЃЈ-2,3ЃЉЃЌЧѓГіжБЯпBNЕФНтЮіЪНЮЊy=3x+9ЃЌЗжСНжжЧщПіЃКЕБЕуHдкOBжЎМфЪБЃЌгЩ![]() ЃЌЕУЕНBNЁЮCHЃЌЕУЕНжБЯпCHЕФНтЮіЪНЮЊy=3x+3ЃЌМДПЩЧѓГіЕуHЕФзјБъЮЊЃЈ-1,0ЃЉЃЛЕБЕуHдкЕуBзѓВрЪБЃЌCHНЛBNгкMЃЌзїжБЯпOMЃЌгЩ
ЃЌЕУЕНBNЁЮCHЃЌЕУЕНжБЯпCHЕФНтЮіЪНЮЊy=3x+3ЃЌМДПЩЧѓГіЕуHЕФзјБъЮЊЃЈ-1,0ЃЉЃЛЕБЕуHдкЕуBзѓВрЪБЃЌCHНЛBNгкMЃЌзїжБЯпOMЃЌгЩ![]() ЕУЕНBM=MCЃЌЙЪOMЪЧBCЕФДЙжБЦНЗжЯпЃЌЧѓГіНЛЕуMЕФзјБъЮЊЃЈ-
ЕУЕНBM=MCЃЌЙЪOMЪЧBCЕФДЙжБЦНЗжЯпЃЌЧѓГіНЛЕуMЕФзјБъЮЊЃЈ-![]() ЃЌ
ЃЌ![]() ЃЉЃЌдйЧѓГіжБЯпCMЕФНтЮіЪНЮЊy=
ЃЉЃЌдйЧѓГіжБЯпCMЕФНтЮіЪНЮЊy=![]() x+3ЃЌМДПЩЕУЕНЕуHЕФзјБъЮЊЃЈ-9,0ЃЉЃЛЂкШчЭМ1ЃЌЕБЕуQдкxжсЯТЗНЧвMHЁЭxжсЪБЃЌMHзюаЁЃЌзїQGЁЭxжсЃЌЙ§ЕуMзїMFЁЭQGгкFЃЌдђЫФБпаЮMHGFЪЧОиаЮЃЌжЄУїЁїBQGЁеЁїQMFЃЌЕУЕНFM=GQЃЌBG=FQЃЌРћгУЙДЙЩЖЈРэЧѓГіGQ=GH=
x+3ЃЌМДПЩЕУЕНЕуHЕФзјБъЮЊЃЈ-9,0ЃЉЃЛЂкШчЭМ1ЃЌЕБЕуQдкxжсЯТЗНЧвMHЁЭxжсЪБЃЌMHзюаЁЃЌзїQGЁЭxжсЃЌЙ§ЕуMзїMFЁЭQGгкFЃЌдђЫФБпаЮMHGFЪЧОиаЮЃЌжЄУїЁїBQGЁеЁїQMFЃЌЕУЕНFM=GQЃЌBG=FQЃЌРћгУЙДЙЩЖЈРэЧѓГіGQ=GH=![]() ЃЌЕУЕНMH=FG=BG-FG=
ЃЌЕУЕНMH=FG=BG-FG=![]() ЃЛШчЭМ2ЃЌЕБЕуQдкxжсЩЯЗНЃЌЧвMHЁЭxжсЪБЃЌMHзюДѓЃЌЙ§ЕуQзїQGЁЭxжсЃЌQFЁЭMHгкFЃЌдђЫФБпаЮHGQFЪЧОиаЮЃЌЭЌРэЃКЁїBGQЁеЁїMFQЃЌЕУЕНQG=FQ=HGЃЌBG=MFЃЌРћгУЙДЙЩЖЈРэЧѓГіGQ=GH=
ЃЛШчЭМ2ЃЌЕБЕуQдкxжсЩЯЗНЃЌЧвMHЁЭxжсЪБЃЌMHзюДѓЃЌЙ§ЕуQзїQGЁЭxжсЃЌQFЁЭMHгкFЃЌдђЫФБпаЮHGQFЪЧОиаЮЃЌЭЌРэЃКЁїBGQЁеЁїMFQЃЌЕУЕНQG=FQ=HGЃЌBG=MFЃЌРћгУЙДЙЩЖЈРэЧѓГіGQ=GH=![]() ЃЌЕУЕНMH=BG+FH=
ЃЌЕУЕНMH=BG+FH=![]() ЃЌМДПЩЕУЕНMHЕФШЁжЕЗЖЮЇ.
ЃЌМДПЩЕУЕНMHЕФШЁжЕЗЖЮЇ.
ЃЈ1ЃЉНЋЕуAЁЂBЕФзјБъДњШы![]() жаЃЌЕУ
жаЃЌЕУ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФБэДяЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБx=0ЪБЃЌy=3ЃЌЁрЕуCЕФзјБъЮЊЃЈ0,3ЃЉЃЌ
Й§ЕуCзїCGЁЭOPгкGЃЌ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Й§ЕуPзїPFЁЭxжсгкFЃЌЙ§ЕуEзїENЁЭPFгкNЃЌ
ЁрENЁЮOFЃЌ
Ёр![]() ,
,
ЩшЕуPЕФзјБъЮЊЃЈaЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрOF=-aЃЌEN=-![]() ЃЌ
ЃЌ
ЁрЕуEЕФКсзјБъЮЊ![]() ЃЌ
ЃЌ
ЁпBЃЈ3,0ЃЉЃЌCЃЈ0,3ЃЉЃЌ
ЁржБЯпBCЕФНтЮіЪНЮЊy=x+3ЃЌ
ЕБx=![]() ЪБЃЌy=
ЪБЃЌy=![]() +3ЃЌ
+3ЃЌ
ЁрEЃЈ![]() ЃЌ
ЃЌ![]() +3ЃЉЃЌ
+3ЃЉЃЌ
Ёп2PF=5PNЃЌ
Ёр5(![]() -
-![]() -3)=2(
-3)=2(![]() ),
),
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЕуPЕФзјБъЮЊЃЈ-1,4ЃЉЛђЃЈ-2,3ЃЉЃЛ
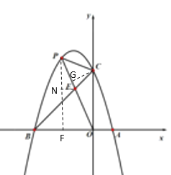
ЃЈ3ЃЉЂйЁп![]()
![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФЖдГЦжсЪЧжБЯпx=-1ЃЌ
ЁпЕу![]() ЙигкХзЮяЯпЖдГЦжсЕФЖдГЦЕуЮЊЕу
ЙигкХзЮяЯпЖдГЦжсЕФЖдГЦЕуЮЊЕу![]() ЃЌCЃЈ0,3ЃЉЃЌ
ЃЌCЃЈ0,3ЃЉЃЌ
ЁрNЃЈ-2,3ЃЉЃЌ
ЩшжБЯпBNЕФНтЮіЪНЮЊy=kx+bЃЌ
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпBNЕФНтЮіЪНЮЊy=3x+9ЃЌ
ЕБЕуHдкOBжЎМфЪБЃЌШчЭМЃЌ
Ёп![]() ЃЌ
ЃЌ
ЁрBNЁЮCHЃЌ
ЩшжБЯпCHЕФНтЮіЪНЮЊy=3x+mЃЌНЋЕуCЕФзјБъДњШыЃЌЕУm=3,
ЁржБЯпCHЕФНтЮіЪНЮЊy=3x+3ЃЌ
ЕБy=0ЪБЃЌЕУx=-1ЃЌ
ЁрЕуHЕФзјБъЮЊЃЈ-1,0ЃЉЃЛ
ЕБЕуHдкЕуBзѓВрЪБЃЌШчЭМЃЌCHНЛBNгкMЃЌзїжБЯпOMЃЌ
Ёп![]() ЃЌ
ЃЌ
ЁрBM=MCЃЌ
ЁпOB=OCЃЌ
ЁрOMЪЧBCЕФДЙжБЦНЗжЯпЃЌ
ЁржБЯпOMЕФНтЮіЪНЮЊy=-xЃЌ
НтЗНГЬзщ![]() ЃЌЕУ
ЃЌЕУ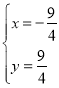 ЃЌ
ЃЌ
ЁрЕуMЕФзјБъЮЊЃЈ-![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЩшжБЯпCMЕФНтЮіЪНЮЊy=cx+nЃЌ
Ёр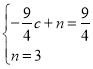 ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
ЁржБЯпCMЕФНтЮіЪНЮЊy=![]() x+3ЃЌ
x+3ЃЌ
ЕБy=0ЪБx=-9ЃЌЁрЕуHЕФзјБъЮЊЃЈ-9,0ЃЉЃЌ
злЩЯЃЌЕБ![]() ЪБЃЌЕуHЕФзјБъЮЊЃЈ-1,0ЃЉЛђЃЈ-9ЃЌ0ЃЉЃЛ
ЪБЃЌЕуHЕФзјБъЮЊЃЈ-1,0ЃЉЛђЃЈ-9ЃЌ0ЃЉЃЛ
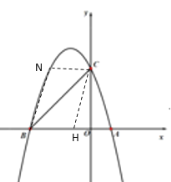
ЂкШчЭМ1ЃЌЕБЕуQдкxжсЯТЗНЧвMHЁЭxжсЪБЃЌMHзюаЁЃЌзїQGЁЭxжсЃЌЙ§ЕуMзїMFЁЭQGгкFЃЌдђЫФБпаЮMHGFЪЧОиаЮЃЌ
ЁрFM=GHЃЌFG=MHЃЌ
ЁпЁЯBQM=ЁЯF=90ЁуЃЌ
ЁрЁЯBQG+ЁЯFQM=ЁЯFMQ+ЁЯFQM=90ЁуЃЌ
ЁрЁЯBQG=ЁЯFMQЃЌ
ЁпЁЯBGQ=ЁЯFЃЌBQ=MQЃЌ
ЁрЁїBQGЁеЁїQMFЃЌ
ЁрFM=GQЃЌBG=FQЃЌ
ЁрGQ=FM=GHЃЌ
ЁпQH=1ЃЌ
ЁрGQ=GH=![]() ЃЌ
ЃЌ
Ёр MH=FG=BG-FG=![]() ЃЛ
ЃЛ
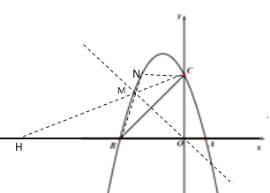
ШчЭМ2ЃЌЕБЕуQдкxжсЩЯЗНЃЌЧвMHЁЭxжсЪБЃЌMHзюДѓЃЌЙ§ЕуQзїQGЁЭxжсЃЌQFЁЭMHгкFЃЌдђЫФБпаЮHGQFЪЧОиаЮЃЌ
ЁрFQ=HGЃЌFH=QGЃЌ
ЭЌРэЃКЁїBGQЁеЁїMFQЃЌ
ЁрQG=FQ=HGЃЌBG=MFЃЌ
ЁпQH=1ЃЌ
ЁрGQ=GH=![]() ЃЌ
ЃЌ
ЁрMH=BG+FH=![]() ЃЌ
ЃЌ
ЁрMHЕФШЁжЕЗЖЮЇЪЧ![]() .
.




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
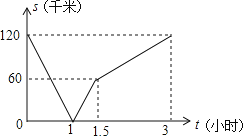
ЁОЬтФПЁПМзЦяФІЭаГЕДгAЕиШЅBЕиЃЌввПЊЦћГЕДгBЕиШЅAЕиЃЌЭЌЪБГіЗЂЃЌдШЫйааЪЛЃЌИїздЕНДяжеЕуКѓЭЃжЙЃЌЩшМзЁЂввСНШЫМфОрРыЮЊsЃЈЕЅЮЛЃКЧЇУзЃЉЃЌМзааЪЛ ЕФЪБМфЮЊtЃЈЕЅЮЛЃКаЁЪБЃЉЃЌsгыtжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЌгаЯТСаНсТлЃКЂйГіЗЂ1аЁЪБЪБЃЌМзЁЂввдкЭОжаЯргіЃЛЂкГіЗЂ1.2аЁЪБЪБЃЌввБШМзЖрааЪЛСЫ50ЧЇУзЃЛЂлввЕНжеЕуЪБЃЌМзРыжеЕуЛЙга60ЧЇУзЃЛЂмМзЕФЫйЖШЪЧввЫйЖШЕФвЛАыЃЎЦфжаЃЌе§ШЗНсТлЪЧ _____________ ЃЎЃЈЬюађКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
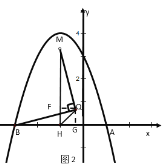
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+bx+2НЛxжсгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉСНЕуЃЌНЛyжсгкЕуCЃЌгыЙ§ЕуCЧвЦНаагкxжсЕФжБЯпНЛгкСэвЛЕуDЃЌЕуPЪЧХзЮяЯпЩЯвЛЖЏЕуЃЎ
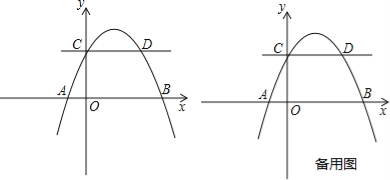
ЃЈ1ЃЉЧѓХзЮяЯпНтЮіЪНМАЕуDзјБъЃЛ
ЃЈ2ЃЉЕуEдкxжсЩЯЃЌШєвдAЃЌEЃЌDЃЌPЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЧѓДЫЪБЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЙ§ЕуPзїжБЯпCDЕФДЙЯпЃЌДЙзуЮЊQЃЌШєНЋЁїCPQбиCPЗелЃЌЕуQЕФЖдгІЕуЮЊQЁфЃЎЪЧЗёДцдкЕуPЃЌЪЙQЁфЧЁКУТфдкxжсЩЯЃПШєДцдкЃЌЧѓГіДЫЪБЕуPЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЪЧЪЕбщЪвжаЕФвЛжжАкЖЏзАжУЃЌBCдкЕиУцЩЯЃЌжЇМмABCЪЧЕзБпЮЊBCЕФЕШбќжБНЧШ§НЧаЮЃЌАкЖЏБлADПЩШЦЕуAа§зЊЃЌАкЖЏБлDMПЩШЦЕуDа§зЊЃЌADЃН30ЃЌDMЃН10ЃЎ

ЃЈ1ЃЉдка§зЊЙ§ГЬжаЃЌ
ЂйЕБAЃЌDЃЌMШ§ЕудкЭЌвЛжБЯпЩЯЪБЃЌЧѓAMЕФГЄЃЎ
ЂкЕБAЃЌDЃЌMШ§ЕуЮЊЭЌвЛжБНЧШ§НЧаЮЕФЖЅЕуЪБЃЌЧѓAMЕФГЄЃЎ
ЃЈ2ЃЉШєАкЖЏБлADЫГЪБеыа§зЊ90ЁуЃЌЕуDЕФЮЛжУгЩЁїABCЭтЕФЕуD1зЊЕНЦфФкЕФЕуD2ДІЃЌСЌНсD1D2ЃЌШчЭМ2ЃЌДЫЪБЁЯAD2CЃН135ЁуЃЌCD2ЃН60ЃЌЧѓBD2ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2019Фъ3дТ12ШеЪЧЕк41ИіжВЪїНкЃЌФГЕЅЮЛЛ§МЋПЊеЙжВЪїЛюЖЏЃЌОіЖЈЙКТђМзЁЂввСНжжЪїУчЃЌгУ800дЊЙКТђМзжжЪїУчЕФПУЪ§гыгУ680дЊЙКТђввжжЪїУчЕФПУЪ§ЯрЭЌЃЌввжжЪїУчУППУБШМзжжЪїУчУППУЩй6дЊЃЎ
ЃЈ1ЃЉЧѓМзжжЪїУчУППУЖрЩйдЊЃП
ЃЈ2ЃЉШєзМБИгУ3800дЊЙКТђМзЁЂввСНжжЪїУчЙВ100ПУЃЌдђжСЩйвЊЙКТђввжжЪїУчЖрЩйПУЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
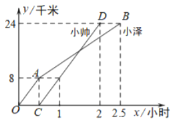
ЁОЬтФПЁПаЁдѓКЭаЁЫЇСНЭЌбЇЗжБ№ДгМзЕиГіЗЂЃЌЦяздааГЕбиЭЌвЛЬѕТЗЕНввЕиВЮМгЩчЛсЪЕМљЛюЖЏЃЎШчЭМелЯп![]() КЭЯпЖЮ
КЭЯпЖЮ![]() ЗжБ№БэЪОаЁдѓКЭаЁЫЇРыМзЕиЕФОрРы
ЗжБ№БэЪОаЁдѓКЭаЁЫЇРыМзЕиЕФОрРы![]() ЃЈЕЅЮЛЃКЧЇУзЃЉгыЪБМф
ЃЈЕЅЮЛЃКЧЇУзЃЉгыЪБМф![]() ЃЈЕЅЮЛЃКаЁЪБЃЉжЎМфКЏЪ§ЙиЯЕЕФЭМЯѓЃЌдђЕБаЁЫЇЕНДяввЕиЪБЃЌаЁдѓОрввЕиЕФОрРыЮЊ_________ЧЇУзЃЎ
ЃЈЕЅЮЛЃКаЁЪБЃЉжЎМфКЏЪ§ЙиЯЕЕФЭМЯѓЃЌдђЕБаЁЫЇЕНДяввЕиЪБЃЌаЁдѓОрввЕиЕФОрРыЮЊ_________ЧЇУзЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯп![]() ЕФВПЗжЭМЯѓШчЭМЫљЪОЃЌгыxжсЕФвЛИіНЛЕузјБъЮЊ
ЕФВПЗжЭМЯѓШчЭМЫљЪОЃЌгыxжсЕФвЛИіНЛЕузјБъЮЊ![]() ЃЌХзЮяЯпЕФЖдГЦжсЪЧ
ЃЌХзЮяЯпЕФЖдГЦжсЪЧ![]() ЯТСаНсТлжаЃК
ЯТСаНсТлжаЃК
![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ![]() ЗНГЬ
ЗНГЬ![]() гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЛ
гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЛ![]() ХзЮяЯпгыxжсЕФСэвЛИіНЛЕузјБъЮЊ
ХзЮяЯпгыxжсЕФСэвЛИіНЛЕузјБъЮЊ![]() ЃЛ
ЃЛ![]() ШєЕу
ШєЕу![]() дкИУХзЮяЯпЩЯЃЌдђ
дкИУХзЮяЯпЩЯЃЌдђ![]() ЃЎ
ЃЎ
Цфжае§ШЗЕФга![]() ЁЁЁЁ
ЁЁЁЁ![]()

A. 5Иі B. 4Иі C. 3Иі D. 2Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЫЎЙћЩЬДгХњЗЂЪаГЁгУ8000дЊЙКНјСЫДѓгЃЬвКЭаЁгЃЬвИї200ЧЇПЫЃЌДѓгЃЬвЕФНјМлБШаЁгЃЬвЕФНјМлУПЧЇПЫЖр20дЊ.ДѓгЃЬвЪлМлЮЊУПЧЇПЫ40дЊЃЌаЁгЃЬвЪлМлЮЊУПЧЇПЫ16дЊ.
(1)ДѓгЃЬвКЭаЁгЃЬвЕФНјМлЗжБ№ЪЧУПЧЇПЫЖрЩйдЊ?ЯњЪлЭъКѓЃЌИУЫЎЙћЩЬЙВзЌСЫЖрЩйдЊЧЎ?
(2)ИУЫЎЙћЩЬЕкЖўДЮШдгУ8000дЊЧЎДгХњЗЂЪаГЁЙКНјСЫДѓгЃЬвКЭаЁгЃЬвИї200ЧЇПЫЃЌНјМлВЛБфЃЌЕЋдкдЫЪфЙ§ГЬжааЁгЃЬвЫ№КФСЫ20%ЃЎШєаЁгЃЬвЕФЪлМлВЛБфЃЌвЊЯыШУЕкЖўДЮзЌЕФЧЎВЛЩйгкЕквЛДЮЫљзЌЧЎЕФ90%ЃЌДѓгЃЬвЕФЪлМлзюЩйгІЮЊЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНааЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() дкЦНааЫФБпаЮ
дкЦНааЫФБпаЮ![]() ЕФБпЩЯЃЌЧв
ЕФБпЩЯЃЌЧв![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌдђЯпЖЮ
ЃЌдђЯпЖЮ![]() ЕФГЄЮЊ__________ЃЎ
ЕФГЄЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com