
【题目】2019年3月12日是第41个植树节,某单位积极开展植树活动,决定购买甲、乙两种树苗,用800元购买甲种树苗的棵数与用680元购买乙种树苗的棵数相同,乙种树苗每棵比甲种树苗每棵少6元.
(1)求甲种树苗每棵多少元?
(2)若准备用3800元购买甲、乙两种树苗共100棵,则至少要购买乙种树苗多少棵?
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】某市电力部门对一般照明用电实行“阶梯电价”收费,具体收费标准如下:
第一档:月用电量不超过240度的部分的电价为每度0.6元;
第二档:月用电量超过240度但不超过400度部分的电价为每度0.65元;
第三档:月用电量超过400度的部分的电价为每度0.9元.
(1)已知老王家去年5月份的用电量为380度,则老王家5月份应交电费 元;
(2)若去年6月份老王家用电的平均电价为0.70元,求老王家去年6月份的用电量;
(3)已知老王家去年7、8月份的用电量共500度(7月份的用电量少于8月份的用电量),两个月的总电价是303元,求老王家7、8月的用电量分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学分别用标有数字0、﹣1、4的三张卡片(除了数字不同以外,其余都相同)做游戏,他们将卡片洗匀后,将标有数字的一面朝下放在桌面上,甲先随机抽取一张,抽出的卡片放回,乙再从三张卡片中随机抽取一张.若规定甲同学抽到卡片上的数字比乙同学抽取到卡片上的数字大,则甲同学获胜;否则乙同学获胜.请你用列表法或画树状图法求哪名同学获胜的概率大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠C=90°,AC=8cm,BC=6cm,M 在 AC上,且AM=6cm,过点 A(与 BC 在 AC 同侧)作射线 AN⊥AC,若动点 P 从点 A 出发,沿射线 AN 匀速运动,运动速度为 1cm/s,设点 P 运动时间为 t 秒.
(1)经过 秒时,Rt△AMP 是等腰直角三角形?
(2)经过几秒时,PM⊥MB?
(3)经过几秒时,PM⊥AB?
(4)当△BMP 是等腰三角形时,直接写出 t 的所有值.

查看答案和解析>>
科目:初中数学 来源: 题型:
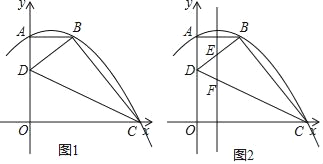
【题目】已知,如图1,O是坐标原点,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,AB⊥y轴于点A,AB=2,AO=4,OC=5,点D是线段AO上一动点,连接CD、BD.
(1)求出抛物线的解析式;
(2)如图2,抛物线的对称轴分别交BD、CD于点E、F,当△DEF为等腰三角形时,求出点D的坐标;
(3)当∠BDC的度数最大时,请直接写出OD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() 、
、![]() 满足
满足![]() .
.


(1)如图1,请求出![]() 、
、![]() 的值以及
的值以及![]() 的度数;
的度数;
(2)如图1,若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 轴正半轴上一动点,连接
轴正半轴上一动点,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 轴于
轴于![]() 点,当
点,当![]() 点在
点在![]() 轴正半轴上运动的过程中,
轴正半轴上运动的过程中,![]() 的值是否发生改变?如发生改变,求出变化范围;若不改变,求该式子的值。
的值是否发生改变?如发生改变,求出变化范围;若不改变,求该式子的值。
(3)如图2,若点![]() 为
为![]() 轴负半轴上一点,连接
轴负半轴上一点,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,请连接
,请连接![]() 并求出
并求出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C(0,4).
(1)求此抛物线的解析式;
(2)设点P(2,n)在此抛物线上,AP交y轴于点E,连接BE,BP,请判断△BEP的形状,并说明理由;
(3)设抛物线的对称轴交x轴于点D,在线段BC上是否存在点Q,使得△DBQ成为等腰直角三角形?若存在,求出点Q的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 边长为
边长为![]() 的等边三角形
的等边三角形![]() 的顶点
的顶点![]() 分别在边
分别在边![]() ,
,![]() 上当
上当![]() 在边
在边![]() 上运动时,
上运动时,![]() 随之在边
随之在边![]() 上运动,等边三角形的形状保持不变,运动过程中,点
上运动,等边三角形的形状保持不变,运动过程中,点![]() 到点
到点![]() 的最大距离为( )
的最大距离为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=3,BC=4.点P在线段AB或线段AD上,点Q中线段BC上,沿直线PQ将矩形折叠,点B的对应点是点E.
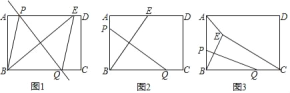
(1)如图1,点P、点E在线段AD上,点Q在线段BC上,连接BP、EQ.
①求证:四边形PBQE是菱形.
②四边形PBQE是菱形时,AP的取值范围是 .
(2)如图2,点P在线段AB上,点Q在线段AD上,点E在线段AD上,若AE=![]() ,求折痕PQ的长.
,求折痕PQ的长.
(3)点P在线段AB,AP=2,点Q在线段BC上,连AE、CE.请直接写出四边形AECD的面积的最小值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com