
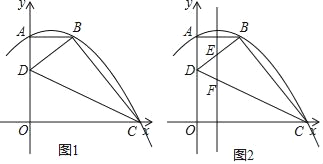
【题目】已知,如图1,O是坐标原点,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,AB⊥y轴于点A,AB=2,AO=4,OC=5,点D是线段AO上一动点,连接CD、BD.
(1)求出抛物线的解析式;
(2)如图2,抛物线的对称轴分别交BD、CD于点E、F,当△DEF为等腰三角形时,求出点D的坐标;
(3)当∠BDC的度数最大时,请直接写出OD的长.
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+4;(2)当△DEF为等腰三角形时,点D的坐标为(0,
x+4;(2)当△DEF为等腰三角形时,点D的坐标为(0,![]() )或(0,
)或(0,![]() )或(0,12﹣2
)或(0,12﹣2![]() );(3)
);(3)![]()
【解析】
(1)先确定出点A,B,C的坐标,进而用待定系数法即可得出结论;
(2)先判断出要△DEF是等腰三角形,即:△BDH是等腰三角形,设出点D坐标,进而表示出BD,DH,BH,分三种情况建立方程求解即可得出结论;
(3)先判断出∠BDC最大时,BD⊥BC,进而利用相似三角形建立方程求解即可得出结论.
(1)∵AB⊥y轴于点A,AB=2,AO=4,OC=5,
∴A(0,4),B(2,4),C(5,0),
∵抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,
∴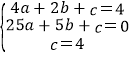 ,
,
∴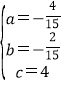 ,
,
∴抛物线解析式为y=-![]() x2-
x2-![]() x+4;
x+4;
(2)如图,
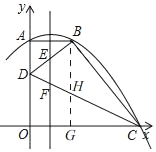
过点B作BG⊥OC于G,交CD于H,
∴点H,G的横坐标为2,
∵EF⊥OC,
∴EF∥BH,
∵△DEF是等腰三角形,
∴△BDH是等腰三角形,
设D(0,5m)(0≤m≤![]() ),
),
∵C(5,0),
∴直线CD的解析式为y=﹣mx+5m,
∴H(2,3m),
∴BH=4﹣3m,
∴BH2=9m2﹣24m+16,DH2=4+(5m﹣3m)2=4+4m2,BD2=4+(5m﹣4)2=25m2﹣40m+20,
当BD=DH时,25m2﹣40m+20=4+4m2,
∴m=![]() (舍)或m=
(舍)或m=![]() ,
,
∴5m=![]() ,
,
∴D(0,![]() ),
),
当BD=BH时,25m2﹣40m+20=9m2﹣24m+16,
∴m=![]() ,
,
∴D(0,![]() ),
),
当BH=DH时,9m2﹣24m+16=4+4m2,
∴m=![]() 或m=
或m=![]() (舍去),
(舍去),
∴D(0,12﹣2![]() ),
),
即:当△DEF为等腰三角形时,点D的坐标为(0,![]() )或(0,
)或(0,![]() )或(0,12﹣2
)或(0,12﹣2![]() );
);
(3)如图1,
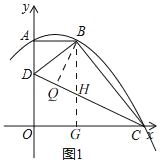
过点B作BG⊥OC于G,交CD于H,
∴四边形OABG是矩形,点H,G的横坐标为2,
∴∠OAB=∠ABG=90°,
∴OG=2,
∵OC=5,
∴CG=3,
∵B(2,4),
∴BG=4,
过点B作BQ⊥CD,
∴∠BQD=90°,
∴要∠BDC最大,
∴∠DBQ最小,
即:BD⊥BC时,∠DBQ最小,
∴∠DBC=90°=∠ABG,
∴∠ABD=∠CBG,
∵∠BGC=∠BAD=90°,
∴△ABD∽△GBC,
∴![]() ,
,
∴![]() ,
,
∴AD=![]() ,
,
∴OD﹣OA﹣AD=![]() .
.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,∠AOB=10°,点P在OB上.以点P为圆心,OP为半径画弧,交OA于点P1(点P1与点O不重合),连接PP1;再以点P1为圆心,OP为半径画弧,交OB于点P2(点P2与点P不重合),连接P1 P2;再以点P2为圆心,OP为半径画弧,交OA于点P3(点P3与点P1不重合),连接P2 P3;……
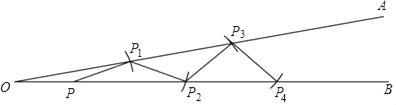
请按照上面的要求继续操作并探究:
∠P3 P2 P4=_____°;按照上面的要求一直画下去,得到点Pn,若之后就不能再画出符合要求点Pn+1了,则n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,DC=5 cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC边上,设落点为F,若△ABF的面积为30 cm2,求△ADE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.

(1)若∠BDA=115°,则∠BAD= °,∠DEC= °;
(2)若DC=AB,求证:△ABD≌△DCE;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
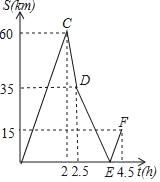
【题目】A、B两地相距150km,甲、乙两人先后从A地出发向B地行驶,甲骑摩托车匀速行驶,乙开汽车且途中速度只改变一次,如图表示的是甲、乙两人之间的距离S关于时间t的函数图象(点F的实际意义是乙开汽车到达B地),请根据图象解答下列问题:
(1)求出甲的速度;
(2)求出乙前后两次的速度,并求出点E的坐标;
(3)当甲、乙两人相距10km时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年3月12日是第41个植树节,某单位积极开展植树活动,决定购买甲、乙两种树苗,用800元购买甲种树苗的棵数与用680元购买乙种树苗的棵数相同,乙种树苗每棵比甲种树苗每棵少6元.
(1)求甲种树苗每棵多少元?
(2)若准备用3800元购买甲、乙两种树苗共100棵,则至少要购买乙种树苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.甲、乙两种商品原来的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,
D为AB边上一点.
(1)求证:△ACE≌△BCD
(2)若AD=6,BD=8,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九(1)、九(2)两班的班长交流了为四川安雅地震灾区捐款的情况:
(Ⅰ)九(1)班班长说:“我们班捐款总数为1200元,我们班人数比你们班多8人.”
(Ⅱ)九(2)班班长说:“我们班捐款总数也为1200元,我们班人均捐款比你们班人均捐款多20%.”
请根据两个班长的对话,求这两个班级每班的人均捐款数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com