
����Ŀ����ͼ������ABC�У�AB��AC����B��40������D���߶�BC���˶���D����B��C�غϣ�������AD������ADE��40����DE���߶�AC�ڵ�E��

��1������BDA��115�������BAD���� ������DEC���� ����
��2����DC��AB����֤����ABD�ա�DCE��
��3���ڵ�D���˶������У���ADE����״�����ǵ����������������ԣ���ֱ��д����BDA�Ķ������������ԣ���˵�����ɣ�
���𰸡���1��25��115����2�������������3������BDA��110���80��ʱ����ADE�ǵ��������Σ�
��������
��1�������������ڽǺͶ���������֪��ֵ���뼴�������BAD������ƽ��Ϊ180���Լ��������ڽǺ�Ϊ180�����������DEC�Ķ�����
��2���������ɵá�EDC����DAB����B����C��DC��AB������ASA����֤�����ۣ�
��3������ADE�ǵ��������Σ���Ϊ����������ٵ�AD��AEʱ����ADE����AED��40�������ݡ�AED����C���ó���ʱ�����ϣ��ڵ�DA��DEʱ�������DAE����DEA��70���������BAC�Ķ��������������ε��ڽǺͶ��������BAD�����������ε��ڽǺͶ��������BDA���ɣ��۵�EA��EDʱ�������DAC�������BAD�Ķ��������������ε��ڽǺͶ��������BDA�Ķ�����
��1���⣺�ߡ�BDA��115������B��40����
���BAD��180������ABD����BDA��180����40����115����25����
��AB��AC����B��40����
���C��40����
�ߡ�BDA+��ADE+��EDC��180������ADE��40������BDA��115����
���EDC��180����115����40����25����
�ߡ�EDC+��C+��DEC��180����
���DEC��180����25����40����115����
�ʴ�Ϊ��25��115��
��2��֤�����ߡ�EDC+��EDA+��ADB��180������DAB+��B+��ADB��180������B����EDA��40����
���EDC����DAB��
�ߡ�B����C��DC��AB��
���ABD�ա�DCE��ASA����
��3���⣺��BDA��80�� ����BDA��110����
��AB��AC��
���B����C��40����
����AD��AEʱ����ADE����AED��40����
�ߡ�AED����C��
����ʱ�����ϣ�
����DA��DEʱ������DAE����DEA��![]() ��180����40������70����
��180����40������70����
�ߡ�BAC��180����40����40����100����
���BAD��100����70����30����
���BDA��180����30����40����110����
����EA��EDʱ����ADE����DAE��40����
���BAD��100����40����60����
���BDA��180����60����40����80����
������BDA��110����80��ʱ����ADE�ǵ��������Σ�


 ��Уͨ��֤��Ч��ҵϵ�д�
��Уͨ��֤��Ч��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90�㣬����C��ֱ��MN��AB��DΪAB����һ�㣬����D��DE��BC����ֱ��MN��E������ΪF������CD��BE��
��1����֤��CE��AD��
��2����D��AB�е�ʱ���ı���BECD��ʲô�����ı��Σ�˵��������ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У��ֱ��Ե�A�͵�BΪԲ�ģ�����![]() AB�ij�Ϊ�뾶�����������ཻ�ڵ�M��N����ֱ��MN����BC�ڵ�D������AD������ADC���ܳ�Ϊ8��AB=6������ABC���ܳ�Ϊ��������
AB�ij�Ϊ�뾶�����������ཻ�ڵ�M��N����ֱ��MN����BC�ڵ�D������AD������ADC���ܳ�Ϊ8��AB=6������ABC���ܳ�Ϊ��������
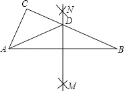
A. 20 B. 22 C. 14 D. 16
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬѧ�ֱ��ñ�������0����1��4�����ſ�Ƭ���������ֲ�ͬ���⣬�����ͬ������Ϸ�����ǽ���Ƭϴ�Ⱥ��������ֵ�һ�泯�·��������ϣ����������ȡһ�ţ�����Ŀ�Ƭ�Żأ����ٴ����ſ�Ƭ�������ȡһ�ţ����涨��ͬѧ�鵽��Ƭ�ϵ����ֱ���ͬѧ��ȡ����Ƭ�ϵ����ִ����ͬѧ��ʤ��������ͬѧ��ʤ���������б�������״ͼ��������ͬѧ��ʤ�ĸ��ʴ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
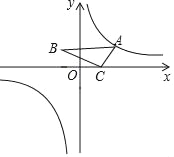
����Ŀ����ͼ��OΪ����ԭ�㣬��C������Ϊ��1��0������ACB=90�㣬��B=30��������A�ڷ���������y=![]() ��ͼ�����˶�ʱ����B�ں���_____���������ʽ����ͼ�����˶���
��ͼ�����˶�ʱ����B�ں���_____���������ʽ����ͼ�����˶���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���� Rt��ABC �У���C��90�㣬AC��8cm��BC��6cm��M �� AC�ϣ���AM��6cm������ A(�� BC �� AC ͬ��)������ AN��AC�������� P �ӵ� A ������������ AN �����˶����˶��ٶ�Ϊ 1cm/s����� P �˶�ʱ��Ϊ t �룮
(1)���� ��ʱ��Rt��AMP �ǵ���ֱ�������Σ�
(2)��������ʱ��PM��MB��
(3)��������ʱ��PM��AB��
(4)����BMP �ǵ���������ʱ��ֱ��д�� t ������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
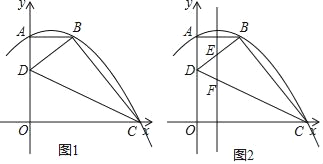
����Ŀ����֪����ͼ1��O������ԭ�㣬������y=ax2+bx+c��a��0������A��B��C���㣬AB��y���ڵ�A��AB=2��AO=4��OC=5����D���߶�AO��һ���㣬����CD��BD��
��1����������ߵĽ���ʽ��
��2����ͼ2�������ߵĶԳ���ֱ�BD��CD�ڵ�E��F������DEFΪ����������ʱ�������D�����ꣻ
��3������BDC�Ķ������ʱ����ֱ��д��OD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+bx+c��a��0����x�ύ�ڵ�A����1��0����B��4��0������y�ύ�ڵ�C��0��4����
��1����������ߵĽ���ʽ��
��2�����P��2��n���ڴ��������ϣ�AP��y���ڵ�E������BE��BP�����ж���BEP����״����˵�����ɣ�
��3���������ߵĶԳ��ύx���ڵ�D�����߶�BC���Ƿ���ڵ�Q��ʹ����DBQ��Ϊ����ֱ�������Σ������ڣ������Q�����ꣻ�������ڣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ�� y=2x+4 �� x ���ཻ�ڵ� A���� y ���ཻ�ڵ� B��

��1���� A��B ��������ꣻ
��2���� B ����ֱ�� BP �� x ���ཻ�� P����ʹ OP=2OA����ֱ�� BP �Ľ���ʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com