
【题目】如图所示,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() 、
、![]() 满足
满足![]() .
.


(1)如图1,请求出![]() 、
、![]() 的值以及
的值以及![]() 的度数;
的度数;
(2)如图1,若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 轴正半轴上一动点,连接
轴正半轴上一动点,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 轴于
轴于![]() 点,当
点,当![]() 点在
点在![]() 轴正半轴上运动的过程中,
轴正半轴上运动的过程中,![]() 的值是否发生改变?如发生改变,求出变化范围;若不改变,求该式子的值。
的值是否发生改变?如发生改变,求出变化范围;若不改变,求该式子的值。
(3)如图2,若点![]() 为
为![]() 轴负半轴上一点,连接
轴负半轴上一点,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,请连接
,请连接![]() 并求出
并求出![]() 的度数.
的度数.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)S△BDM
;(2)S△BDM![]() S△ADN的值不发生改变,S△BDM
S△ADN的值不发生改变,S△BDM![]() S△AND=4;(3)∠OHP=45°.
S△AND=4;(3)∠OHP=45°.
【解析】
(1)由![]() ,求出a、b的值,然后得到OA=OB,则△OAB是等腰直角三角形,即可得到
,求出a、b的值,然后得到OA=OB,则△OAB是等腰直角三角形,即可得到![]() 的度数;
的度数;
(2)连接OD,易证△ODM≌△ADN,从而有S△ODM=S△ADN,由此可得![]() =S△BDM-S△ODM=S△BOD=
=S△BDM-S△ODM=S△BOD=![]() S△AOB=4;
S△AOB=4;
(3)根据题意,先证明△OAP≌△OBC(ASA),得到OP=OC,过O分别作OM⊥CB于M点,作ON⊥HA于N点,得到△COM≌△PON,得到OM=ON,则HO平分∠CHA,即可得到![]() 的度数.
的度数.
解:(1)∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴点A为(4,0),点B为(0,![]() ),
),
∴OA=OB=4,
∴△OAB是等腰直角三角形,
∴![]() ;
;
(2)S△BDM![]() S△ADN的值不发生改变,等于4.
S△ADN的值不发生改变,等于4.
理由如下:连接OD,如图:

∵∠AOB=90°,OA=OB,D为AB的中点,
∴OD⊥AB,∠BOD=∠AOD=45°,OD=DA=BD
∴∠OAD=45°,∠MOD=90°+45°=135°,
∴∠DAN=135°=∠MOD.
∵MD⊥ND即∠MDN=90°,
∴∠MDO=∠NDA=90°![]() ∠MDA.
∠MDA.
在△ODM与△ADN中,
 ,
,
∴△ODM≌△ADN(ASA),
∴S△ODM=S△AND
∴S△BDM![]() S△AND
S△AND
=S△BDM![]() S△ODM
S△ODM
=S△BOD=![]() S△AOB
S△AOB
=![]() AOBO
AOBO
=![]() ;
;
(3)如图:

∵AH⊥BC即∠AHC=90°,∠COB=90°
∴∠HAC+∠ACH=∠OBC+∠OCB=90°,
∴∠HAC=∠OBC.
在△OAP与△OBC中,
 ,
,
∴△OAP≌△OBC(ASA),
∴OP=OC=1,
过O分别作OM⊥CB于M点,作ON⊥HA于N点,如图:

在四边形OMHN中,∠MON=360°![]() 3×90°=90°,
3×90°=90°,
∴∠COM=∠PON=90°![]() ∠MOP.
∠MOP.
在△COM与△PON中,
 ,
,
∴△COM≌△PON(AAS),
∴OM=ON.
∵OM⊥CB,ON⊥HA,
∴HO平分∠CHA,
∴∠OHP=![]() ∠CHA=45°.
∠CHA=45°.


科目:初中数学 来源: 题型:
【题目】如图,AB=BC,AB⊥BC,过点B作直线l,过点A作AE⊥l于E,过点C作CF⊥l于F,则下列说法中正确的是( )

A.AC=AE+BEB.EF=AE+EBC.AC=EB+CFD.EF=EB+CF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC(AC<AB<BC),用尺规在线段BC上确定一点P,使得PA+PC=BC,则符合要求的作图痕迹是( )

A.如图① 以B为圆心,BA长为半径画弧交BC于点P
B.如图②作AC中垂线交BC于点P
C.如图③以C为圆心,CA 长为半径画弧交BC于点P
D.如图④作AB中垂线交BC于P
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年3月12日是第41个植树节,某单位积极开展植树活动,决定购买甲、乙两种树苗,用800元购买甲种树苗的棵数与用680元购买乙种树苗的棵数相同,乙种树苗每棵比甲种树苗每棵少6元.
(1)求甲种树苗每棵多少元?
(2)若准备用3800元购买甲、乙两种树苗共100棵,则至少要购买乙种树苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试探究AB,AD,DC之间的等量关系,证明你的结论;
(2)如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,证明你的结论.
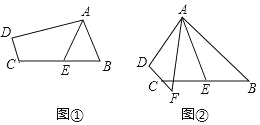
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】烟台享有“苹果之乡”的美誉.甲、乙两超市分别用3000元以相同的进价购进质量相同的苹果.甲超市销售方案是:将苹果按大小分类包装销售,其中大苹果400千克,以进价的2倍价格销售,剩下的小苹果以高于进价10%销售.乙超市的销售方案是:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利2100元(其它成本不计).问:
(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.

(1)当∠BDA=115°时,∠EDC=____ __,∠DEC=__ ___;点D从B向C运动时,∠BAD逐渐变_______(填“大”或“小”),∠BAD_______∠CDE(填“=”或“>”或“<”).
(2)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com