
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.

(1)当∠BDA=115°时,∠EDC=____ __,∠DEC=__ ___;点D从B向C运动时,∠BAD逐渐变_______(填“大”或“小”),∠BAD_______∠CDE(填“=”或“>”或“<”).
(2)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
【答案】(1)25°,115°,大;=;(2)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形.
【解析】
(1)根据∠BDA=115°以及∠ADE=40°,即可得出∠EDC=180°∠BDA∠ADE,进而求出∠DEC的度数;然后观察图形,根据三角形内角和定理及平角的概念可得∠BAD逐渐变大,∠BAD=∠CDE;
(2)分情况讨论:①当AD=AE时,②当DA=DE时,③当EA=ED时,分别利用三角形外角的性质和三角形内角和定理进行求解即可.
解:(1)∠EDC=180°∠BDA∠ADE=180°115°40°=25°,
∠DEC=180°∠EDC∠C=180°25°40°=115°;
观察图形可得:点D从B向C运动时,∠BAD逐渐变大,
在△ABD中,∠BAD=180°-∠ABD-∠BDA=180°-40°-∠BDA,
∵∠CDE=180°-∠BDA-∠ADE=180°-40°-∠BDA,
∴∠BAD=∠CDE;
故答案为:25°,115°,大;=;
(2)分情况讨论:
①当AD=AE时,则∠ADE=∠AED=40°,
∵∠AED>∠C=40°,
∴此情况不成立;
②当DA=DE时,即∠DAE=∠DEA=![]() (180°40°)=70°,
(180°40°)=70°,
∠BDA=∠DAE+∠C=70°+40°=110°;
③当EA=ED时,∠ADE=∠DAE=40°,
∠BDA=∠DAE+∠C=40°+40°=80°,
综上所述:当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=8, BC=4,将长方形的一角沿AC折叠,则重叠阴影部分△AFC的面积为( )

A. 14B. 12C.10D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() 、
、![]() 满足
满足![]() .
.


(1)如图1,请求出![]() 、
、![]() 的值以及
的值以及![]() 的度数;
的度数;
(2)如图1,若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 轴正半轴上一动点,连接
轴正半轴上一动点,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 轴于
轴于![]() 点,当
点,当![]() 点在
点在![]() 轴正半轴上运动的过程中,
轴正半轴上运动的过程中,![]() 的值是否发生改变?如发生改变,求出变化范围;若不改变,求该式子的值。
的值是否发生改变?如发生改变,求出变化范围;若不改变,求该式子的值。
(3)如图2,若点![]() 为
为![]() 轴负半轴上一点,连接
轴负半轴上一点,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,请连接
,请连接![]() 并求出
并求出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,K是正方形ABCD内一点,以AK为一边作正方形AKLM,使L,M,D在AK的同旁,连接BK和DM,试用旋转的思想说明线段BK与DM的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 边长为
边长为![]() 的等边三角形
的等边三角形![]() 的顶点
的顶点![]() 分别在边
分别在边![]() ,
,![]() 上当
上当![]() 在边
在边![]() 上运动时,
上运动时,![]() 随之在边
随之在边![]() 上运动,等边三角形的形状保持不变,运动过程中,点
上运动,等边三角形的形状保持不变,运动过程中,点![]() 到点
到点![]() 的最大距离为( )
的最大距离为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
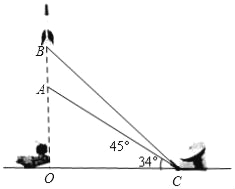
【题目】如图,雷达站C处检测到一枚由地面垂直升空的巡航导弹,导弹以240m/s的速度,用10秒从点A飞行到点B,在C处测得点A,B的仰角分别为34°和45°,求导弹发射位置O与雷达站C之间的距离(结果精确到0.1km),(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,在矩形 ABCD 中,动点 E 从点 B 出发,沿 B→C→D→A 方向运动至点 A 处停止,设点 E 运动的路程为 x,△ABE 的面积为 y,如果 y 关于 x 的函数图象如图 2 所示,则当 x=10 时,点 E应运动到( )

A.A 处B.B 处C.C 处D.D 处
查看答案和解析>>
科目:初中数学 来源: 题型:
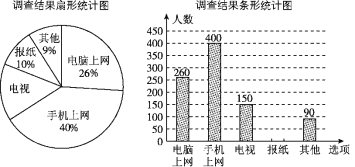
【题目】为了了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调查结果绘制了如图所示尚不完整的统计图.
根据图中信息解答下列问题:
(1)这次接受调查的市民总人数是________;
(2)扇形统计图中,“电视”所在扇形的圆心角的度数是________;
(3)请补全条形统计图;
(4)若该市约有80万人,请你估计其中将“电脑上网和手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com