练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，K是正方形ABCD内一点，以AK为一边作正方形AKLM，使L，M，D在AK的同旁，连接BK和DM，试用旋转的思想说明线段BK与DM的关系．

    【答案】BK与DM的关系是互相垂直且相等，理由见解析.

    【解析】试题分析:用旋转的方法解答本题,将△ABK绕A逆时针旋转90°后与△ADM重合,可证明△ABK和△ADM全等,BK和DM是对应边,然后根据全等三角形的性质可以证明BK与DM的关系是互相垂直且相等.

    试题解析:BK与DM的关系是互相垂直且相等,

    ∵四边形ABCD和四边形AKLM都是正方形,

    ∴AB=AD,AK=AM,∠BAK=90°﹣∠DAK,∠DAM=90°﹣∠DAK,

    ∴∠BAK=∠DAM,

    ,

    ∴△ABK≌△ADM（SAS）,

    把△ABK绕A逆时针旋转90°后与△ADM重合,

    ∴BK=DM且BK⊥DM.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠C＝90°，以A为圆心，任意长为半径画弧分别交AB，AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于点P，连接AP并延长交BC于点D，则下列结论：①AD是∠BAC的平分线；②若∠B＝30°，则DA＝DB；③AB：AC＝2:1；④点D在AB的垂直平分线上．一定成立的个数为（ ）

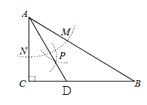
    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若抛物线y=x2-2x+c与y轴的交点为（0，-3），则下列说法不正确的是（ ）

    A．抛物线开口向上

    B．抛物线的对称轴是x=1

    C．当x=1时，y的最大值为-4

    D．抛物线与x轴的交点为（-1，0），（3，0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知等腰三角形ABC中，AB=AC，点D,E分别在边AB、AC上，且AD=AE，连接BE、CD，交于点F.

    (1)求证：∠ABE＝∠ACD；

    (2)求证：过点A、F的直线垂直平分线段BC.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在某地，人们发现在一定温度下某种蟋蟀叫的次数与温度之间有如下的竟是关系：

    （1）在这个变化过程中，自变量是 ，因变量是 ；

    （2）在当地温度每增加，这种蟋蟀叫的次数是怎样变化的？

    （3）这种蟋蟀叫的次数（次）与当地温度之间的关系为 ；

    （4）当这种蟋蟀叫的次数时，求当时该地的温度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（10分）水果店张阿姨以每斤2元的价格购进某种水果若干斤，然后以每斤4元的价格出售，每天可售出100斤，通过调查发现，这种水果每斤的售价每降低0.1元，每天可多售出20斤，为保证每天至少售出260斤，张阿姨决定降价销售．

    （1）若将这种水果每斤的售价降低x元，则每天的销售量是 斤（用含x的代数式表示）；

    （2）销售这种水果要想每天盈利300元，张阿姨需将每斤的售价降低多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下图的转盘被划分成六个相同大小的扇形，并分别标上1，2，3，4，5，6这六个数字，指针停在每个扇形的可能性相等。四位同学各自发表了下述见解：

    甲：如果指针前三次都停在了3号扇形，下次就一定不会停在3号扇形；

    乙：只要指针连续转六次，一定会有一次停在6号扇形；

    丙：指针停在奇数号扇形的概率与停在偶数号扇形的概率相等；

    丁：运气好的时候，只要在转动前默默想好让指针停在6号扇形，指针停在6号扇形的可能性就会加大。

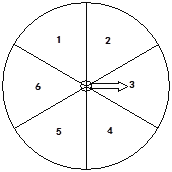
    其中，你认为正确的见解有（ ）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题中，正确的有（ ）

    ①Rt△ABC中，已知两边长分别为3和4，则第三边长为5；

    ②有一个内角等于其他两个内角和的三角形是直角三角形；

    ③三角形的三边分别为a，b，C，若a2+c2=b2，那么∠C=90°；

    ④若△ABC中，∠A：∠B：∠C=1：5：6，则△ABC是直角三角形．

    A．1个 B．2个 C．3个 D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】正方形网格中（网格中的每个小正方形边长是1），△ABC的顶点均在格点上，请在所给的直角坐标系中解答下列问题：

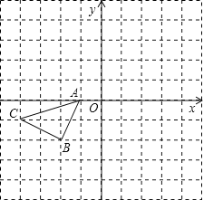
    （1）作出△ABC绕点A逆时针旋转90°的△AB1C1．

    （2）作出△AB1C1关于原点O成中心对称的△A1B2C2．

    （3）请直接写出以A1、B2、C2为顶点的平行四边形的第四个顶点D的坐标．

    查看答案和解析>>

    同步练习册答案