【题目】如图，在
中，
，
为
边的中点，
为等边三角形.
（1）求证：
；
（2）若
，在
边上找一点
，使得
最小，并求出这个最小值.
【答案】（1）证明见解析；（2）
的最小值为3.
【解析】
（1）根据直角三角形的性质可得：
，然后根据等边三角形的性质可得：
，从而得出
，然后利用SAS即可证出：
.
（2）作点
关于直线
的对称点
，连接
交于点
，根据两点之间线段最短，此时
最小，为的长，则最小，为
. 则点H即为所求，然后根据等边三角形的判定可证出
为等边三角形，从而得出
是直角三角形，最后根据勾股定理，即可求出的最小值.
（1）证明：在
中，
，为
边的中点，
∴.
∵
为等边三角形，
∴.
∴
.
∴.
在△ADE和△CDB中
∴
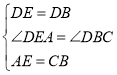
（2）如图，作点关于直线的对称点，连接交于点，
根据两点之间线段最短，此时最小，为的长，
则最小，为. 则点H即为所求.
在中，
，
∴
，则
.
∴∠
∠EAC=60°
∴为等边三角形
∴
∴是直角三角形
∴
.
∴的最小值为3
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目：初中数学 来源： 题型：
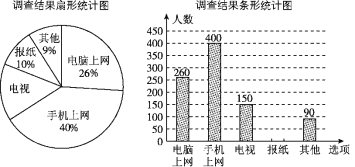
【题目】如图所示，直线
交
轴于点
，交
轴于点
，且
、
满足
.
（1）如图1，请求出、的值以及
的度数；
（2）如图1，若点
为的中点，点
为轴正半轴上一动点，连接
，过作
交轴于
点，当点在轴正半轴上运动的过程中，
的值是否发生改变？如发生改变，求出变化范围；若不改变，求该式子的值。
（3）如图2，若点
为
轴负半轴上一点，连接
，过点
作
于点
，
交
于点
，请连接
并求出
的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图 1，在矩形 ABCD 中，动点 E 从点 B 出发，沿 B→C→D→A 方向运动至点 A 处停止，设点 E 运动的路程为 x，△ABE 的面积为 y，如果 y 关于 x 的函数图象如图 2 所示，则当 x=10 时，点 E应运动到（ ）
A.A 处B.B 处C.C 处D.D 处
查看答案和解析>>
科目：初中数学 来源： 题型：
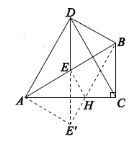
【题目】为了了解市民“获取新闻的最主要途径”，某市记者开展了一次抽样调查，根据调查结果绘制了如图所示尚不完整的统计图．
根据图中信息解答下列问题：
(1)这次接受调查的市民总人数是________；
(2)扇形统计图中，“电视”所在扇形的圆心角的度数是________；
(3)请补全条形统计图；
(4)若该市约有80万人，请你估计其中将“电脑上网和手机上网”作为“获取新闻的最主要途径”的总人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】矩形ABCD中，AB=3，BC=4．点P在线段AB或线段AD上，点Q中线段BC上，沿直线PQ将矩形折叠，点B的对应点是点E．
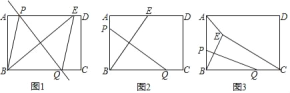
（1）如图1，点P、点E在线段AD上，点Q在线段BC上，连接BP、EQ．
①求证：四边形PBQE是菱形．
②四边形PBQE是菱形时，AP的取值范围是 ．
（2）如图2，点P在线段AB上，点Q在线段AD上，点E在线段AD上，若AE=
，求折痕PQ的长．
（3）点P在线段AB，AP=2，点Q在线段BC上，连AE、CE．请直接写出四边形AECD的面积的最小值是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
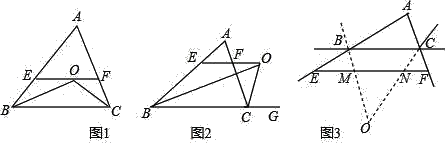
【题目】已知，如图1：△ABC中，∠B、∠C的平分线相交于点O，过点O作EF∥BC交AB、AC于E、F
（1）直接写出图1中所有的等腰三角形．指出EF与BE、CF间有怎样的数量关系？
（2）在（1）的条件下，若AB=15，AC=10，求△AEF的周长；
（3）如图2，若△ABC中，∠B的平分线与三角形外角∠ACG的平分线CO交于点O，过O点作OE∥BC交AB于E，交AC于F，请问（1）中EF与BE、CF间的关系还是否存在，若存在，说明理由：若不存在，写出三者新的数量关系，并说明理由；
（4）如图3，∠ABC、∠ACB的外角平分线的延长线相交于点O，请直接写出EF，BE，CF，MN之间的数量关系．不需证明．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
