
����Ŀ����ͼ����ʾ����ƽ��ֱ������ϵ�У�������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() Ϊ�������ߵĶ��㣮
Ϊ�������ߵĶ��㣮
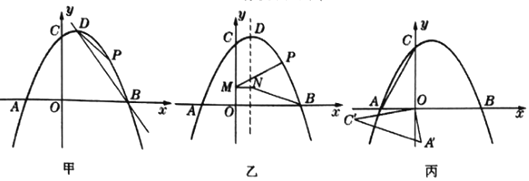
��1����ͼ�ף���![]() Ϊ��������
��������![]() ��
��![]() ������һ���㣬����
������һ���㣬����![]() ��
��![]() ����
����![]() ������ʱ���ڶԳ�������һ����
������ʱ���ڶԳ�������һ����![]() ����ͼ����ʾ������
����ͼ����ʾ������![]() ��
��![]() �ύ
�ύ![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ����
����![]() ����Сֵ���������ʱ��
����Сֵ���������ʱ��![]() �����ꣻ
�����ꣻ
��2����ͼ����ʾ����![]() ���ŵ�
���ŵ�![]() ��ת���õ�
��ת���õ�![]() ������ת�����У��Ƿ����ij��ʱ��ʹ�Ե�
������ת�����У��Ƿ����ij��ʱ��ʹ�Ե�![]() Ϊ�����������Ϊ��
Ϊ�����������Ϊ��![]() Ϊ���ĵ��������Σ�������ڣ���ֱ��д����ʱ��
Ϊ���ĵ��������Σ�������ڣ���ֱ��д����ʱ��![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]()
![]() ��
��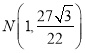 ����2��
����2��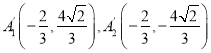 ��
��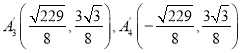 ��
��
��������
��1������![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() �����õ�
�����õ�![]() ������ö��κ��������ʵõ���
������ö��κ��������ʵõ���![]() �����꣬��
�����꣬��![]() ����ƽ��һ����λ��ʹ��
����ƽ��һ����λ��ʹ��![]() �ڵ�
�ڵ�![]() �غϣ���
�غϣ���![]() ����
����![]() ���ϵĵ�
���ϵĵ�![]() ������
������![]() ����
����![]() ��ԳƵĵ�Ϊ
��ԳƵĵ�Ϊ![]() ����ʱ
����ʱ![]() ��С����СֵΪ
��С����СֵΪ![]() ���Ӷ��ɵô𰸣�
���Ӷ��ɵô𰸣�
��2����ת�����з�����������ۣ���![]() ʱ����
ʱ����![]() ����
����![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() �������������ε����ʱ�ʾ
�������������ε����ʱ�ʾ![]() �����꣬���ù��ɶ����������������ɵô𰸣���
�����꣬���ù��ɶ����������������ɵô𰸣���![]() ͬ���ɵô𰸣�
ͬ���ɵô𰸣�
�⣺��1������![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]()
��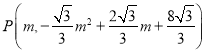 ��
��
![]() ��
��
![]() ��
��![]()
![]()
��![]()
![]()
![]()
��ã�![]()
![]()
��![]() Ϊ
Ϊ![]()
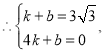
��ã�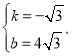
![]() Ϊ
Ϊ![]()
![]()
![]() ��
��
![]()
![]()
�൱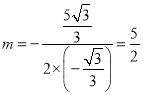 ʱ��
ʱ��![]() ���ʱ
���ʱ![]() �����Ҳ���
�����Ҳ���
��ʱ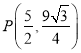
��![]() ����ƽ��һ����λ��ʹ��
����ƽ��һ����λ��ʹ��![]() �ڵ�
�ڵ�![]() �غϣ���
�غϣ���![]() ����
����![]() ���ϵĵ�
���ϵĵ�![]() ����
����
��![]() ����
����![]() ��ԳƵĵ�Ϊ
��ԳƵĵ�Ϊ![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
��ʱ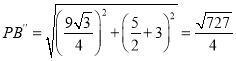
![]()
![]()
![]() ��
��
![]()
![]() Ϊ
Ϊ![]() ��
��
![]()
��ʱ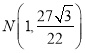
��2��������֪��![]()
![]()
��![]() ʱ��
ʱ��
��ͼ����![]() ����
����![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
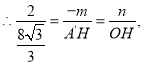
![]()
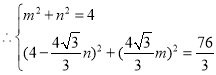
��ã�
![]() ��
��![]()
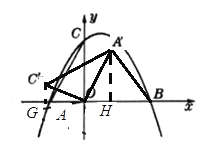
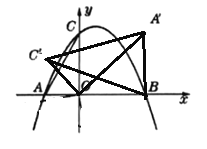
��ͼ����![]()
ͬ���ɵã�
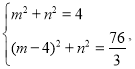
��ã�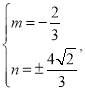
![]() ��
��![]() ��
��
���ϣ�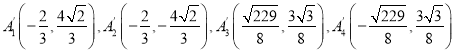


 ���ݼ���ϵ�д�
���ݼ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �ı߳�Ϊ8��
�ı߳�Ϊ8��![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() ���ϵĶ��㣬����
���ϵĶ��㣬����![]() ���Ե�
���Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() ��Ϊ�뾶��
��Ϊ�뾶��![]() .
.
��1����![]() ________ʱ��
________ʱ��![]() ��
��
��2����![]() ��������
��������![]() �ı�����ʱ����
�ı�����ʱ����![]() �ij���
�ij���

��3����![]() �İ뾶Ϊ
�İ뾶Ϊ![]() ����ֱ��д��������
����ֱ��д��������![]() ��ǡ��������������Բ�ڵ�
��ǡ��������������Բ�ڵ�![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
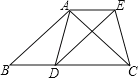
����Ŀ����֪����ͼ������ABC�У�AB=AC��DΪ��BC��һ�㣬��AB��BDΪ�ڱ���ƽ���ı���ABDE������AD��EC��
��1����֤��AD=CE��
��2������D��ʲôλ��ʱ���ı���ADCE�Ǿ��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
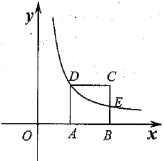
����Ŀ����ͼ���߳�Ϊ2��������![]() �Ķ���
�Ķ���![]() ��
��![]() ���������ϣ�����������
���������ϣ�����������![]() ��ͼ���ڵ�һ����ͼ����
��ͼ���ڵ�һ����ͼ����![]() ����
����![]() ��
��![]() .
.
(1)����![]() ������Ϊ
������Ϊ![]() ʱ����
ʱ����![]() ��
��![]() ��ֵ;
��ֵ;
(2)����![]() ��
��![]() ���е㣬��
���е㣬��![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С��ͬѧ��ʵ�����е��������ͬ��Ũ�Ȳ�ͬ�Ļ�ѧ��Ӧ�Լ�![]() ��Һ����֪С����С�Ƶ��Ƶ�
��Һ����֪С����С�Ƶ��Ƶ�![]() ��ҺŨ�ȷֱ�Ϊ
��ҺŨ�ȷֱ�Ϊ![]() ��
��![]() ���ֽ�С�����Ƶ�
���ֽ�С�����Ƶ�![]() ��Һ��
��Һ��![]() ����С�Ƶ��Ƶ�
����С�Ƶ��Ƶ�![]() ��Һ�У���Ͼ��Ⱥ�����С�Ƶ��Ƶ�
��Һ�У���Ͼ��Ⱥ�����С�Ƶ��Ƶ�![]() ��Һ����С�����Ƶ�
��Һ����С�����Ƶ�![]() ��Һʹ������ָ���ԭ���������С����С�Ƶ��Ƶ�
��Һʹ������ָ���ԭ���������С����С�Ƶ��Ƶ�![]() ��Һ����
��Һ����![]() ���IJ��뻥��ǰС����С�Ƶ��Ƶ�
���IJ��뻥��ǰС����С�Ƶ��Ƶ�![]() ��Һ����
��Һ����![]() ���IJ�֮��Ϊ_______��
���IJ�֮��Ϊ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
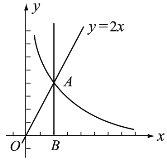
����Ŀ����ͼ����![]() ��ֱ��
��ֱ��![]() �뷴��������
�뷴��������![]() ��
��![]() Ϊ��������ͼ��Ľ��㣮����
Ϊ��������ͼ��Ľ��㣮����![]() ��
��![]() ��Ĵ��ߣ�����Ϊ
��Ĵ��ߣ�����Ϊ![]() ����
����![]() ��
��
��1�����![]() �����꼰
�����꼰![]() ��ֵ��
��ֵ��
��2����֪��![]() ������
������![]() ��ƽ����
��ƽ����![]() ���ֱ�ߣ���ֱ��
���ֱ�ߣ���ֱ��![]() �ڵ�
�ڵ�![]() ��������������
��������������![]() ��
��![]() Ϊ��������ͼ���ڵ�
Ϊ��������ͼ���ڵ�![]() ��������
��������![]() �ڵ�
�ڵ�![]() ����
����![]() ����Ϻ�����ͼ��ֱ��д��
����Ϻ�����ͼ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
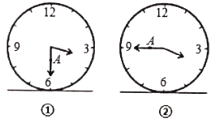
����Ŀ��ͼ�ٱ�ʾһ��ʱ�ӵ����洹ֱ�̶���ˮƽ�����ϣ����з�������һ��A����������ʾ3��30��ʱ�����봹ֱ�����棬A�������ĸ߶�Ϊ10cm��ͼ�ڱ�ʾ��������ʾ3��45��ʱ��A�������ĸ߶�Ϊ16cm����������ʾ3��55��ʱ��A�������ĸ߶�Ϊ____![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
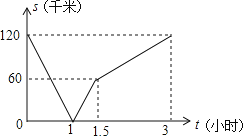
����Ŀ������Ħ�г���A��ȥB�أ��ҿ�������B��ȥA�أ�ͬʱ������������ʻ�����Ե����յ��ֹͣ����ס������˼����Ϊs����λ��ǧ�ף�������ʻ ��ʱ��Ϊt����λ��Сʱ����s��t֮��ĺ�����ϵ��ͼ��ʾ�������н��ۣ��ٳ���1Сʱʱ���ס�����;���������ڳ���1.2Сʱʱ���ұȼ���ʻ��50ǧ�ף����ҵ��յ�ʱ�������յ㻹��60ǧ�ף��ܼ��ٶ������ٶȵ�һ�룮���У���ȷ������ _____________ ��������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
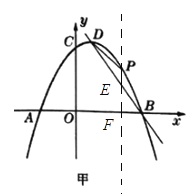
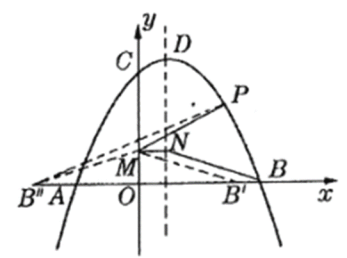
����Ŀ����ͼ��������y=ax2+bx+2��x����A����1��0����B��4��0�����㣬��y���ڵ�C�������C��ƽ����x���ֱ�߽�����һ��D����P����������һ���㣮
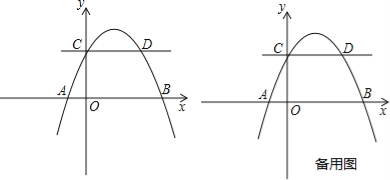
��1���������߽���ʽ����D���ꣻ
��2����E��x���ϣ�����A��E��D��PΪ������ı�����ƽ���ı��Σ����ʱ��P�����ꣻ
��3������P��ֱ��CD�Ĵ��ߣ�����ΪQ��������CPQ��CP���ۣ���Q�Ķ�Ӧ��ΪQ�����Ƿ���ڵ�P��ʹQ��ǡ������x���ϣ������ڣ������ʱ��P�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com