【题目】已知：如图，在△ABC中，AB=AC，D为边BC上一点，以AB，BD为邻边作平行四边形ABDE，连接AD，EC．

（1）求证：AD=CE；

（2）当点D在什么位置时，四边形ADCE是矩形，请说明理由．

参考答案：

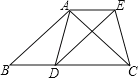
【答案】（1）证明见解析；（2）点D在BC的中点上时，四边形ADCE是矩形，理由见解析.

【解析】试题分析：(1)、根据平移得到AD平行且等于DE，∠B=∠EDC，根据AB=AC得出∠B=∠ACD，AC=DE，结合DC=CD得到△ACD和△ECD全等，得出AD=EC；(2)、首先得出四边形ADCE是平行四边形，结合AD⊥BC得出矩形.

试题解析：(1)、由平移可得AB∥DE，AB=DE； ∴∠B=∠EDC∵ AB=AC ∴∠B=∠ACD， AC=DE

∴∠EDC =∠ACD ∵DC=CD ∴△ACD≌△ECD（SAS） ∴AD="EC"

(2)、当点D是BC中点时,四边形ADCE是矩形

理由如下：∵AB=AC，点D是BC中点 ∴BD=DC，AD⊥BC

由平移性质可知 四边形ABDE是平行四边形 ∴AE=BD，AE∥BD ∴AE=DC，AE∥DC

∴四边形ADCE是平行四边形 ∵AD⊥BC ∴四边形ADCE是矩形

关闭