
【题目】如图,正方形![]() 的边长为8,
的边长为8,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 边上的动点,连结
边上的动点,连结![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径作
长为半径作![]() .
.
(1)当![]() ________时,
________时,![]() ;
;
(2)当![]() 与正方形
与正方形![]() 的边相切时,求
的边相切时,求![]() 的长;
的长;

(3)设![]() 的半径为
的半径为![]() ,请直接写出正方形
,请直接写出正方形![]() 中恰好有两个顶点在圆内的
中恰好有两个顶点在圆内的![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 的长为3或
的长为3或![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据相似三角形对应边成比例列出方程即可解答;
(2)⊙P与正方形ABCD的边相切时有两种情况,分别是与CD边和AD边相切,分别画出图形,用勾股定理即可解答;
(3)因为B点始终在圆内,所以正方形ABCD中恰好有两个顶点在圆内,是C在圆内,D点在圆上或园外,求出它们的极值即可解答
(1)∵∠B=∠C=90°,ΔMBPΔDCP;
∴![]()
设BP=x,则CP=4-x,
∵AB=CD=8,BP=![]() =4
=4
∴![]()
![]() ,
,
(2)解:如图1,当![]() 与边
与边![]() 相切时,
相切时,

设![]() ,
,
在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
如图2,当![]() 与边
与边![]() 相切时,
相切时,

设切点为![]() ,连接
,连接![]() ,
,
则![]() ,四边形
,四边形![]() 是矩形.
是矩形.
∴![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() .
.
综上所述,![]() 的长为3或
的长为3或![]() .
.
(3)![]() .
.
如图1,当![]() 时,
时,![]() 经过点
经过点![]() ,点
,点![]() ;
;
如图3,当![]() 经过点
经过点![]() ,点
,点![]() 时
时

∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴⊙P的半径为x,当![]() ,正方形ABCD中恰好有两个顶点在圆内
,正方形ABCD中恰好有两个顶点在圆内


科目:初中数学 来源: 题型:
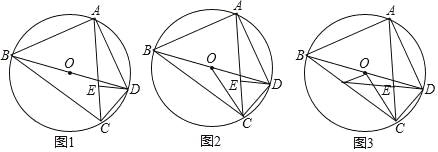
【题目】如图:四边形![]() 为
为![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() 为
为![]() 的直径,
的直径,![]() 于点
于点![]() .
.
(1)如图,求证:![]() ;
;
(2)如图,连接![]() ,当
,当![]() 时,求证:
时,求证:![]() ;
;
(3)如图,在(2)的条件下,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
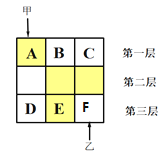
【题目】如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.
(1)若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是多少;
(2)若甲、乙均可在本层移动,用画树状图法或列表法求出黑色方块所构成拼图是轴对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
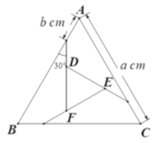
【题目】如图,把边长为![]() cm的等边
cm的等边![]() 剪成四部分,从三角形三个顶点往下bcm处,呈30°角下剪刀,使中间部分形成一个小的等边
剪成四部分,从三角形三个顶点往下bcm处,呈30°角下剪刀,使中间部分形成一个小的等边![]() .若
.若![]() 的面积是
的面积是![]() 的
的![]() ,则
,则![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
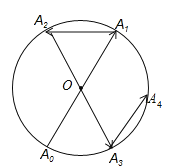
【题目】如图所示,一动点从半径为2的![]() 上的
上的![]() 点出发,沿着射线
点出发,沿着射线![]() 方向运动到
方向运动到![]() 上的点
上的点![]() 处,再向左沿着与射线
处,再向左沿着与射线![]() 夹角为
夹角为![]() 的方向运动到
的方向运动到![]() 上的点
上的点![]() 处;接着又从
处;接着又从![]() 点出发,沿着射线
点出发,沿着射线![]() 方向运动到
方向运动到![]() 上的点
上的点![]() 处,再向左沿着与射线
处,再向左沿着与射线![]() 夹角为
夹角为![]() 的方向运动到
的方向运动到![]() 上的点
上的点![]() 处;
处;![]() 间的距离是________;…按此规律运动到点
间的距离是________;…按此规律运动到点![]() 处,则点
处,则点![]() 与点
与点![]() 间的距离是________.
间的距离是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
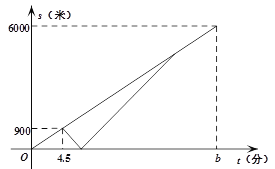
【题目】周末,甲、乙两名大学生骑自行车去距学校6000米的净月潭公园.两人同时从学校出发,以a米/分的速度匀速行驶出发4.5分钟时,甲同学发现忘记带学生证,以1.5a米/分的速度按原路返回学校,取完学生证(在学校取学生证所用时间忽略不计),继续以返回时的速度追赶乙.甲追上乙后,两人以相同的速度前往净月潭.乙骑自行车的速度始终不变.设甲、乙两名大学生距学校的路程为s(米),乙同学行驶的时间为t(分),s与t之间的函数图象如图所示.
(1)求a、b的值.
(2)求甲追上乙时,距学校的路程.
(3)当两人相距500米时,直接写出t的值是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
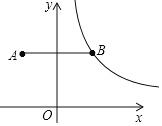
【题目】在平面直角坐标系中,点A(-2,3)关于y轴的对称点为点B,连接AB,反比例函数y=![]() (x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点.
(x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点.
(1)求k的值;
(2)若△ABP的面积等于2,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
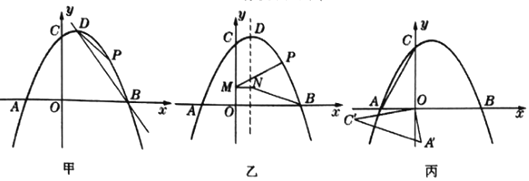
【题目】如图甲所示,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为该抛物线的顶点.
为该抛物线的顶点.
(1)如图甲,点![]() 为抛物线上
为抛物线上![]() ,
,![]() 两点间的一动点,连接
两点间的一动点,连接![]() ,
,![]() ,当
,当![]() 面积最大时,在对称轴上有一动点
面积最大时,在对称轴上有一动点![]() ,如图乙所示,过点
,如图乙所示,过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() ,求
,求![]() 的最小值,并求出此时点
的最小值,并求出此时点![]() 的坐标;
的坐标;
(2)如图丙所示,将![]() 绕着点
绕着点![]() 旋转,得到
旋转,得到![]() ,在旋转过程中,是否存在某个时刻使以点
,在旋转过程中,是否存在某个时刻使以点![]() 为顶点的三角形为以
为顶点的三角形为以![]() 为腰的等腰三角形,如果存在,请直接写出此时点
为腰的等腰三角形,如果存在,请直接写出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com