
【题目】周末,甲、乙两名大学生骑自行车去距学校6000米的净月潭公园.两人同时从学校出发,以a米/分的速度匀速行驶出发4.5分钟时,甲同学发现忘记带学生证,以1.5a米/分的速度按原路返回学校,取完学生证(在学校取学生证所用时间忽略不计),继续以返回时的速度追赶乙.甲追上乙后,两人以相同的速度前往净月潭.乙骑自行车的速度始终不变.设甲、乙两名大学生距学校的路程为s(米),乙同学行驶的时间为t(分),s与t之间的函数图象如图所示.
(1)求a、b的值.
(2)求甲追上乙时,距学校的路程.
(3)当两人相距500米时,直接写出t的值是_______________.
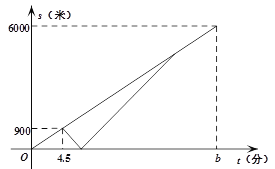
【答案】(1)a=200,b=30;(2)4500米;(3)5.5或17.5
【解析】试题分析:(1)根据速度=路程÷时间,即可解决问题.(2)首先求出甲返回用的时间,再列出方程即可解决问题.(3)分两种情形列出方程即可解决问题.
试题解析:(1)由题意a=![]() =200,b=
=200,b=![]() =30,
=30,
∴a=200,b=30.
(2)![]() +4.5=7.5,
+4.5=7.5,
设t分钟甲追上乙,由题意,300(t7.5)=200t,
解得t=22.5,
22.5×200=4500,
∴甲追上乙时,距学校的路程4500米。
(3)两人相距500米是的时间为t分钟。
由题意:1.5×200(t4.5)+200(t4.5)=500,解得t=5.5分钟,
或300(t7.5)+500=200t,解得t=17.5分钟,
故答案为5.5分钟或17.5分钟。


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
【题目】对于平面内给定射线OA,射线OB及∠MON,给出如下定义:若由射线OA、OB组成的∠AOB的平分线OT落在∠MON的内部或边OM、ON上,则称射线OA与射线OB关于∠MON内含对称.例如,图1中射线OA与射线OB关于∠MON内含对称

已知:如图2,在平面内,∠AOM=10°,∠MON=20°
(1)若有两条射线![]() ,
,![]() 的位置如图3所示,且
的位置如图3所示,且![]() ,
,![]() ,则在这两条射线中,与射线OA关于∠MON内含对称的射线是_____________
,则在这两条射线中,与射线OA关于∠MON内含对称的射线是_____________
(2)射线OC是平面上绕点O旋转的一条动射线,若射线OA与射线OC关于∠MON内含对称,设∠COM=x°,求x的取值范围;
(3)如图4,∠AOE=∠EOH=2∠FOH=20°,现将射线OH绕点O以每秒1°的速度顺时针旋转,同时将射线OE和OF绕点O都以每秒3°的速度顺时针旋转.设旋转的时间为t秒,且![]() .若∠FOE的内部及两边至少存在一条以O为顶点的射线与射线OH关于∠MON内含对称,直接写出t的取值范围.
.若∠FOE的内部及两边至少存在一条以O为顶点的射线与射线OH关于∠MON内含对称,直接写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买若干台电脑,现从两家商场了解到同一种型号的电脑报价均为6000元,并且多买都有一定的优惠.各商场的优惠条件如下表所示:
商场 | 优惠条件 |
甲商场 | 第一台按原价收费,其余的每台优惠25% |
乙商场 | 每台优惠20% |
(1)设学校购买![]() 台电脑,选择甲商场时,所需费用为
台电脑,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 与
与![]() 之间的关系式.
之间的关系式.
(2)什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?
(3)现在因为急需,计划从甲乙两商场一共买入10台电脑,已知甲商场的运费为每台50元,乙商场的运费为每台60元,设总运费为![]() 元,从甲商场购买
元,从甲商场购买![]() 台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把两个全等的等腰直角三角板ABC和EFG(其直角边长均为4)叠放在一起(如图1),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合,现将三角板EFG绕O点顺时针旋转,旋转角![]() 满足条件
满足条件![]() 四边形CHGK是旋转过程中两三角板的重叠部分(如图2).
四边形CHGK是旋转过程中两三角板的重叠部分(如图2).
(1)在上述旋转过程中,BH与CK有怎样的数量关系?证明你的结论;
(2)在上述旋转过程中,两个直角三角形的重叠部分面积是否会发生改变?证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,AB⊥AC,点E是BC的中点,AE与BD交于点F,且F是AE的中点.
(Ⅰ)求证:四边形AECD是菱形;(Ⅱ)若AC=4,AB=5,求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
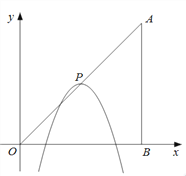
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(6,6)、(6,0).抛物线![]() 的顶点P在折线OAAB上运动.
的顶点P在折线OAAB上运动.
(1)当点P在线段OA上运动时,抛物线![]() 与y轴交点坐标为(0,c).
与y轴交点坐标为(0,c).
①用含m的代数式表示n;
②求c的取值范围;
(2)当抛物线![]() 经过点B时,求抛物线所对应的函数表达式.
经过点B时,求抛物线所对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】读句画图并完成计算:如图,直线AB与直线CD交于点C ,

(1)过点P作PQ∥CD,交AB于点Q;
(2)过P作PR⊥CD于点R;
(3)若∠DCB=150,求∠PQC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购. 经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com