
����Ŀ��������ȫ�ȵĵ���ֱ�����ǰ�ABC��EFG(��ֱ�DZ߳���Ϊ4)������һ��(��ͼ1)����ʹ���ǰ�EFG��ֱ�Ƕ���G�����ǰ�ABC��б���е�O�غϣ��ֽ����ǰ�EFG��O��˳ʱ����ת����ת��![]() ��������
��������![]() �ı���CHGK����ת�����������ǰ���ص�����(��ͼ2).
�ı���CHGK����ת�����������ǰ���ص�����(��ͼ2).
(1)��������ת�����У�BH��CK��������������ϵ��֤����Ľ��ۣ�
(2)��������ת�����У�����ֱ�������ε��ص���������Ƿ�ᷢ���ı䣿֤����Ľ���.

���𰸡�������
��������
�������������֤��������CGK��������BGHȫ�ȣ��Ӷ��ó����ǵ������ȣ��������ı���CHGK�����ת����������CGB�����Ҳ����������ABC�����һ�룬�ɴ˿ɵó��ı���CHGK�������4�����Բ���ı�.
���������BH=CK.�ı���CHGK�����û�б仯.�ߡ�ABC�ǵ���ֱ��������,OΪб���е�,
��CG=BG,CG��AB,���ACG=��B=45��,�ߡ�BGH����CGK��Ϊ��ת��,���BGH=��CGK,
�����CGK���Կ���������BGH�Ƶ�O˳ʱ����ת����,��BH=CK,S��CGK=S��BGH,
��S�ı���CHGK=S��CGK+S��CGH=S��BGH+S��CGH=S��BCG=![]() S��ABC=
S��ABC=![]() ��
��![]() ��4��4=4.
��4��4=4.
���ı���CHGK���������ת������û�б仯,ʼ��Ϊ4.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
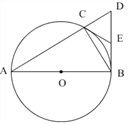
����Ŀ����ͼ����֪��ABC�ڽ��ڡ�O��ABΪ��O��ֱ����BD��AB����AC���ӳ����ڵ�D��
��1����E��BD���е㣬����CE�����ж�CE���O��λ�ù�ϵ��
��2����AC=3CD�����A�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����4������ֱ�������֩�1��2����3��4�IJ�����Ƭ�����dz�����������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ��4�ſ�Ƭ���������һ�Ų��Żأ����ÿ�Ƭ�ϵ����ּ�Ϊm���������ȡ1�ţ�����Ƭ�����ּ�Ϊn��
��1�������б�����״ͼ�ķ�ʽ�ѣ�m��n�����еĽ����ʾ������
��2����ѡ���ģ�m��n���ڶ��������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֤:��ƽ�����ϵĵ㵽����ǵ����ߵľ������.
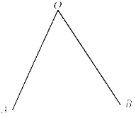
Ҫ��:(1)�߹���ͼ:����AOB�Ľ�ƽ���ߣ����ڸý�ƽ������ȡ��P����PM��OA�ڵ�M��PN��OB�ڵ�N(��д������������ͼ�ۼ�)��
(2)�����ǽ��Ҫ֤�������ͼ��д������֪����֤���������֤������.
��֪:��ͼ��OPƽ�֡�AOB��PM��OA�ڵ�M��PN��OB�ڵ�N.
��֤:PM=PN
֤��:
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ������1���D2��3���D4��5���D6��7���� ���������ų�������ʽ��
��1�� 1
��2�� ��2�� 3
��3�� ��4�� 5�� ��6
��4�� 7�� ��8�� ��9�� ��10
��5�� 11 ��12�� 13�� ��14�� 15
�� ��
����������������ȥ����ô��10�д��������5��������
A.50B.��50C.60D.��60
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
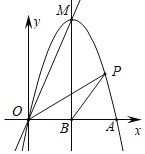
����Ŀ����ͼ��������y��ax2+bx��a��0����x���������ڵ�A��ֱ��y��2x���������ߵĶ���M����֪�������ߵĶԳ���Ϊֱ��x��2����x���ڵ�B��
��1����M������꼰a��b��ֵ��
��2��P�ǵ�һ�������������ϵ�һ�㣬���ڶԳ�����Ҳ࣬����OP��BP�����P�ĺ�����Ϊm����OBP�����ΪS����mΪ����ʱ��s��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
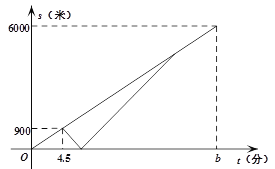
����Ŀ����ĩ���ס���������ѧ�������г�ȥ��ѧУ6000�ľ���̶��.����ͬʱ��ѧУ��������a��/�ֵ��ٶ�������ʻ����4.5����ʱ����ͬѧ�������Ǵ�ѧ��֤����1.5a��/�ֵ��ٶȰ�ԭ·����ѧУ��ȡ��ѧ��֤����ѧУȡѧ��֤����ʱ����Բ��ƣ��������Է���ʱ���ٶ�����.�����Һ���������ͬ���ٶ�ǰ������̶.�������г����ٶ�ʼ�ղ���.��ס���������ѧ����ѧУ��·��Ϊs���ף�����ͬѧ��ʻ��ʱ��Ϊt���֣���s��t֮��ĺ���ͼ����ͼ��ʾ.
��1����a��b��ֵ.
��2���������ʱ����ѧУ��·��.
��3�����������500��ʱ��ֱ��д��t��ֵ��_______________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
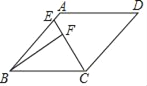
����Ŀ����ͼ��������ABCD�У���ABC=45�㣬AB=4����E��AB���ϵĶ��㣬����B��ֱ��CE�Ĵ��ߣ�����Ϊ��F��
��1������F����AB��ʱ������BCF�Ķ�����
��2������EBF=15�㣬��CF�ij���
��3������E�ӵ�A�˶�����Bʱ�����F�˶���·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ���ש��ͼ�������ִ�ש�������������̳�һ��2��2��������ͼ������ͼ�ڣ�������������Բ����5��������̳�һ��3��3��������ͼ������ͼ�ۣ�������������Բ����13��������̳�һ��4��4��������ͼ������ͼ�ܣ�������������Բ����25�����������̳�һ��15��15��������ͼ����������������Բ���У�����������
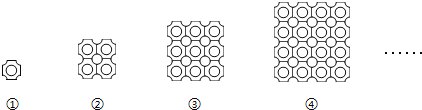
A.365B.366C.420D.421
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com