
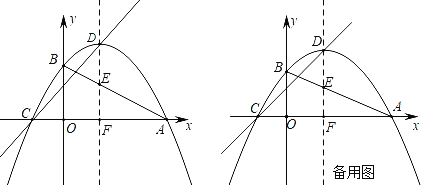
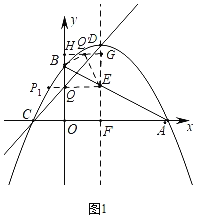
【题目】如图,抛物线y=ax2+x+c与x轴交于点A(6,0),C(﹣2,0),与y轴交于点B,抛物线的顶点为D,对称轴交AB于点E,交x轴于点F.
(1)求抛物线的解析式;
(2)P是抛物线上对称轴左侧一点,连接EP,若tan∠BEP=![]() ,求点P的坐标;
,求点P的坐标;
(3)M是直线CD上一点,N是抛物线上一点,试判断是否存在这样的点N,使得以点B,E,M,N为顶点的四边形是平行四边形,若存在,请直接写出点N的坐标,若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+x+3;(2)点P的坐标为(2﹣2
x2+x+3;(2)点P的坐标为(2﹣2![]() ,2)或(
,2)或(![]() ,
,![]() );(3)存在,满足条件的N点坐标为(4,3)或(﹣4,﹣5)或(2
);(3)存在,满足条件的N点坐标为(4,3)或(﹣4,﹣5)或(2![]() ,1+2
,1+2![]() )或(﹣2
)或(﹣2![]() ,1﹣2
,1﹣2![]() ).
).
【解析】
(1)将点A(6,0),C(﹣2,0)代入y=ax2+x+c即可求解析式;
(2)求出直线AB、CD的解析式,点E的坐标(2,2),由已知可得∠BEP=∠BAO,分两种情况求P点坐标:①过点E作EQ∥x轴交抛物线于点P1,交y轴于点Q,当y=2时求P1点坐标;②作点Q关于AB的对称点Q',连接BQ',EQ',过点Q'作Q'H⊥y轴于点H,过点E作EG⊥Q'H于点G,可以证明△BHQ'∽△Q'GE,得到![]() ,设BH=m,则Q'G=2m,GE=m+1,HQ'=
,设BH=m,则Q'G=2m,GE=m+1,HQ'=![]() (m+1),由HQ'+Q'G=HG=2,求出m=
(m+1),由HQ'+Q'G=HG=2,求出m=![]() ,可求Q'(
,可求Q'(![]() ,
,![]() ),直线EQ'的解析式为y=﹣
),直线EQ'的解析式为y=﹣![]() x+
x+![]() ,联立方程组并解答,即可求P点坐标;
,联立方程组并解答,即可求P点坐标;
(3)由平行四边形对角线互相平分,分两种情况求解:①BE∥MN时,BN的中点与EM的中点重合;②当BM∥NE时,BE的中点与MN的中点重合;建立关系式求出N点坐标.
解:(1)将点A(6,0),C(﹣2,0)代入y=ax2+x+c,
则有![]() ,
,
∴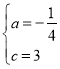 ,
,
∴抛物线的解析式为y=﹣![]() x2+x+3;
x2+x+3;
(2)由题可求B(0,3),D(2,4),
设直线AB的解析式为y=k1x+b1,
将A(6,0),B(0,3)代入可得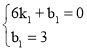 ,
,
∴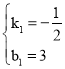 ,
,
∴y=﹣![]() x+3,
x+3,
设直线CD的解析式为y=k2x+b2,
将C(﹣2,0),D(2,4)代入可得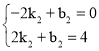 ,
,
∴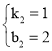 ,
,
∴y=x+2,
∵抛物线的对称轴为x=2,
∴E(2,2),
∴tan∠BAO=![]() ,
,
∵tan∠BEP=![]() ,
,
∴∠BEP=∠BAO,
①如图1:过点E作EQ∥x轴交抛物线于点P1,交y轴于点Q,
当y=2时,﹣![]() x2+x+3=2,
x2+x+3=2,
解得x=2﹣2![]() 或x=2+2
或x=2+2![]() (舍),
(舍),
∴P1(2﹣2![]() ,2);
,2);
②在①中,点Q坐标为(0,2),作点Q关于AB的对称点Q',连接BQ',EQ',
则BQ'=BQ=1,EQ'=EQ=2,
过点Q'作Q'H⊥y轴于点H,过点E作EG⊥Q'H于点G,
∵∠BQ'E=90°,
∴∠BQ'H=90°﹣∠GQ'E=∠Q'EG,
∵∠BHQ'=∠Q'GE=90°,
∴△BHQ'∽△Q'GE,
∴![]() ,
,
∴设BH=m,则Q'G=2m,GE=m+3﹣2=m+1,HQ'=![]() (m+1),
(m+1),
∵HQ'+Q'G=HG=2,
∴![]() (m+1)+2m=2,
(m+1)+2m=2,
∴m=![]() ,
,
∴HO=![]() ,HQ'=
,HQ'=![]() ,
,
∴Q'(![]() ,
,![]() ),
),
易得直线EQ'的解析式为y=﹣![]() x+
x+![]() ,
,
解方程组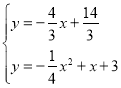 ,
,
解得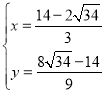 或
或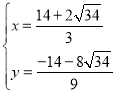 (舍),
(舍),
∴P2(![]() ,
,![]() );
);
综上所述:点P的坐标为(2﹣2![]() ,2)或(
,2)或(![]() ,
,![]() );
);
(3)∵M是直线CD上一点,N是抛物线上一点,
设M(m,m+2),N(x,﹣![]() x2+x+3),已知B(0,3),E(2,2),
x2+x+3),已知B(0,3),E(2,2),
①当BE∥MN时,BN的中点为(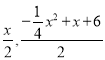 ),ME的中点为(
),ME的中点为(![]() ,
,![]() ),
),
∴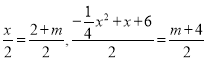 ,
,
∴x=±4,
∴N(4,3)或N(﹣4,﹣5);
②当BM∥NE时,BE的中点为(1,![]() ),MN的中点为(
),MN的中点为(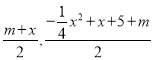 ),
),
∴![]() =1,
=1,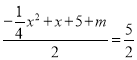 ,
,
∴x=±2![]() ,
,
∴N(2![]() ,1+2
,1+2![]() )或N(﹣2
)或N(﹣2![]() ,1﹣2
,1﹣2![]() );
);
综上所述:满足条件的N点坐标为(4,3)或(﹣4,﹣5)或(2![]() ,1+2
,1+2![]() )或(﹣2
)或(﹣2![]() ,1﹣2
,1﹣2![]() ).
).


科目:初中数学 来源: 题型:
【题目】(问题情境)定义:如图1,点E在四边形ABCD的边CD上,若AE、BE将四边形ABCD分割成三个相似的三角形,则称点E为该四边形的相似点.

(1)若相似点在四边形ABCD的边CD上, 且AE、BE将四边形ABCD分割成三个正三角形,则四边形ABCD的四边形之比(按边长从小到大排序)为_______.
(2)若相似点在四边形ABCD的边CD上,且AE、BE将四边形ABCD分割成三个全等的等腰直角三角形,则四边形ABCD的四边形之比(按边长从小到大排序)为_______.
(3)(探索研究)
如图2,点E为四边形ABCD边上的相似点,且AE、BE将四边形ABCD分割成三个全等的三角形,已知∠ABC=90°,AD=AB=BC=2,求边CD的长.
(4)(问题解决)
如图3,在四边形ABCD中,AB∥CD,点E为四边形ABCD的边CD上的相似点,且AD=a,AB=b,BC=c(其中a≠c),此时边CD的长为多少?请用含a、b、c的代数式直接写出所有可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
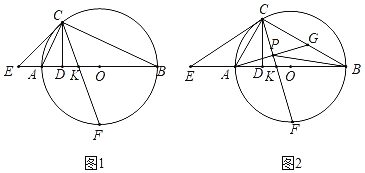
【题目】如图1,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D,E是BA廷长线上一点,连接CE,∠ACE=∠ACD,K是线段AO上一点,连接CK并延长交⊙O于点F.
(1)求证:CE是⊙O的切线;
(2)若AD=DK,求证:AKAO=KBAE;
(3)如图2,若AE=AK,![]() ,点G是BC的中点,AG与CF交于点P,连接BP.请猜想PA,PB,PF的数量关系,并证明.
,点G是BC的中点,AG与CF交于点P,连接BP.请猜想PA,PB,PF的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承优秀传统文化,某校团委组织了一次全校1000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了200名学生的成绩(成绩![]() 取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩 | 频数 | 频率 |
| 10 | 0.05 |
| 20 | 0.10 |
| 30 |
|
|
| 0.30 |
| 80 | 0.40 |
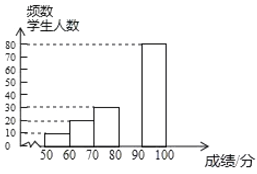
请根据所给的信息,解答下列问题:
(1)![]() _____,
_____,![]() _____;
_____;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在______分数段;
(4)若成绩在90分以上(包括90分)的为优等,则该校参加这次比赛的1000名学生中成绩优等的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
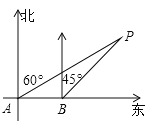
【题目】如图,大海中某灯塔P周围10海里范围内有暗礁,一艘海轮在点A处观察灯塔P在北偏东60°方向,该海轮向正东方向航行8海里到达点B处,这时观察灯塔P恰好在北偏东45°方向.如果海轮继续向正东方向航行,会有触礁的危险吗?试说明理由.(参考数据:![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,tan∠A=![]() ,M,N分别在AD,BC上,将四边形AMNB沿MN翻折,使AB的对应线段EF经过顶点D,当EF⊥AD时,
,M,N分别在AD,BC上,将四边形AMNB沿MN翻折,使AB的对应线段EF经过顶点D,当EF⊥AD时,![]() 的值为_____.
的值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com